【図解】オペアンプ4つの演算回路
この記事では、オペアンプを使った演算回路(加算回路、減算回路、微分回路、積分回路)について解説しています。
動画はこちら↓
加算回路
加算回路は、複数の信号を合成するときに使用する回路で、主に複数のセンサを接続する場合に使用されます。
回路構成
加算回路では、反転増幅回路を基本としつつ、複数の信号源をオペアンプの反転入力端子に接続します。
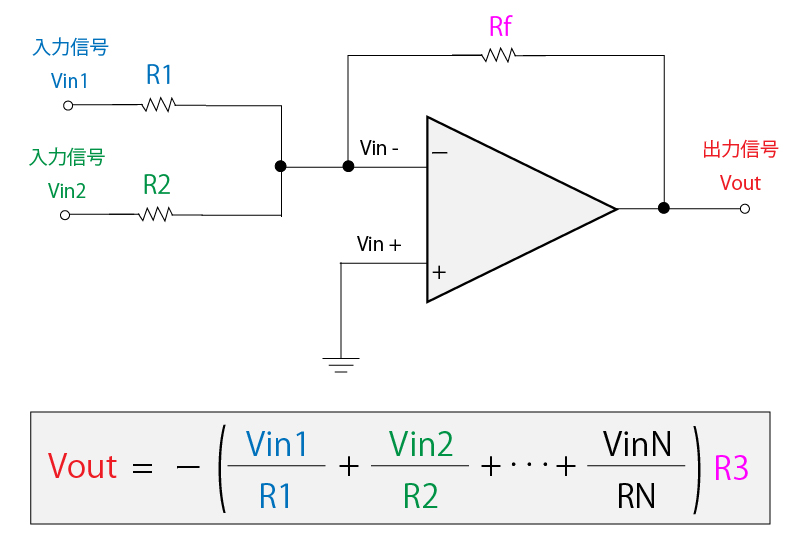
この回路では、それぞれの入力信号が反転増幅回路によって増幅された電圧が出力され、「R1=R2=Rf」の場合には増幅率が 1倍となるため、入力信号同士が足し合わされた出力信号となります。
解析例
2つの入力信号(V1=1V、V2=5V)を加算回路に接続します。
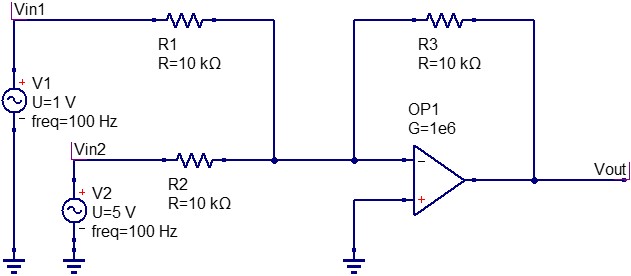
この回路においては「R1=R2=Rf」となっているため、入力信号が足し合わされて、かつ極性が反転した信号が出力されます。
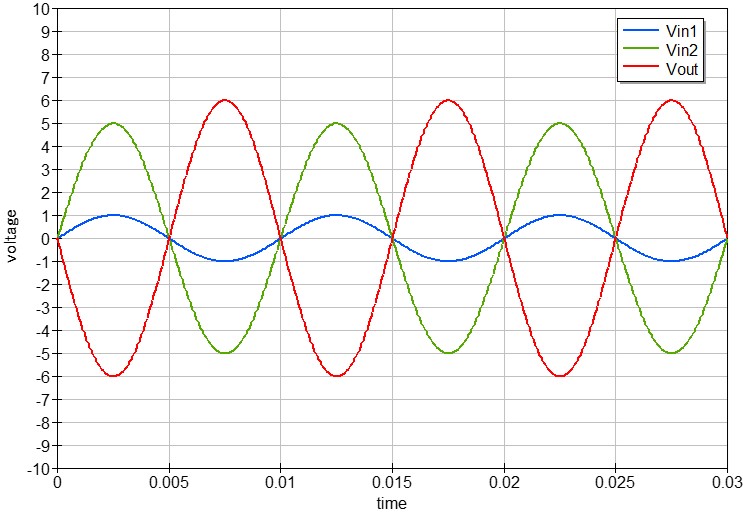
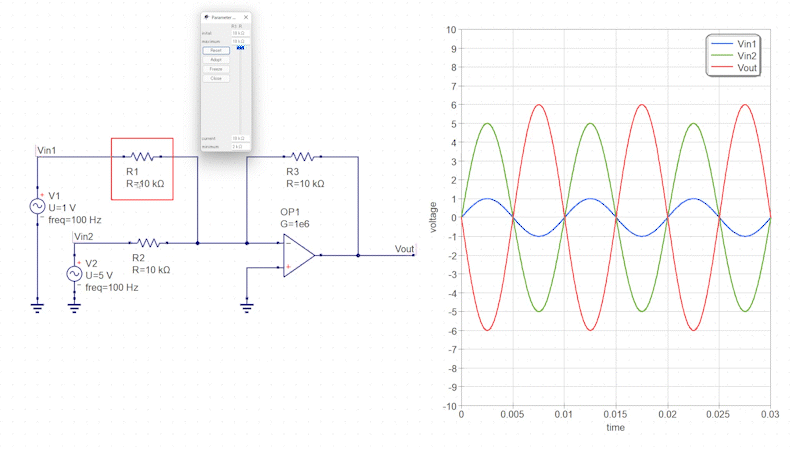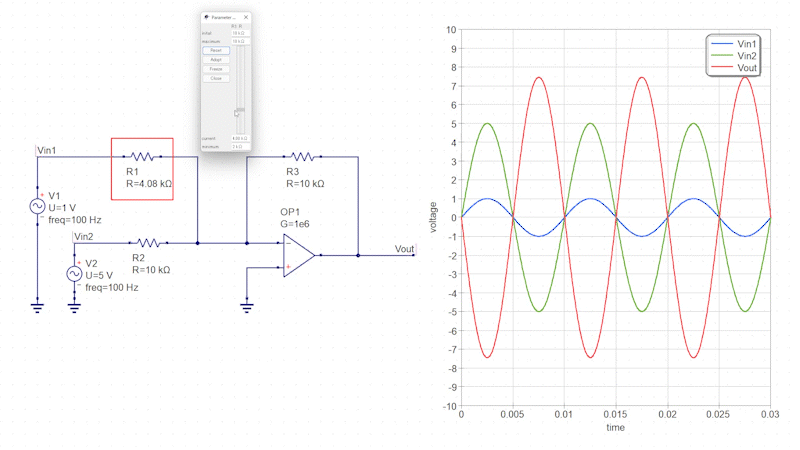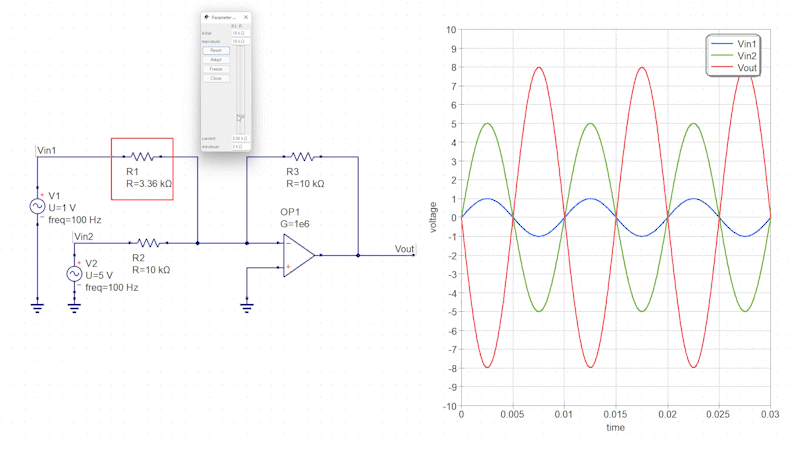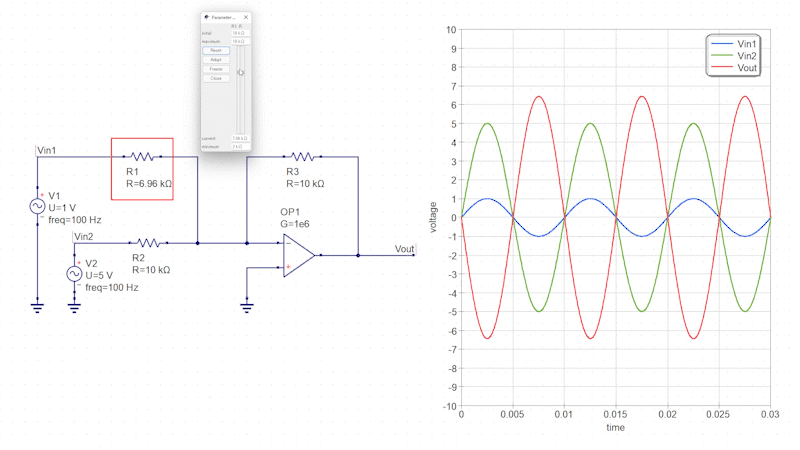
またこの回路では、一方の入力信号の抵抗値(反転増幅回路のゲイン)を調整することで、入力信号ごとに感度を調整することも可能です。

減算回路
減算回路は、2つの信号の差分を増幅する回路で、差動伝送方式の信号検出に使用されます。
回路構成
減算回路では、差動増幅回路をベースとしつつ、増幅率が 1倍となるように抵抗を「R1=R2=R3=R4」とします。
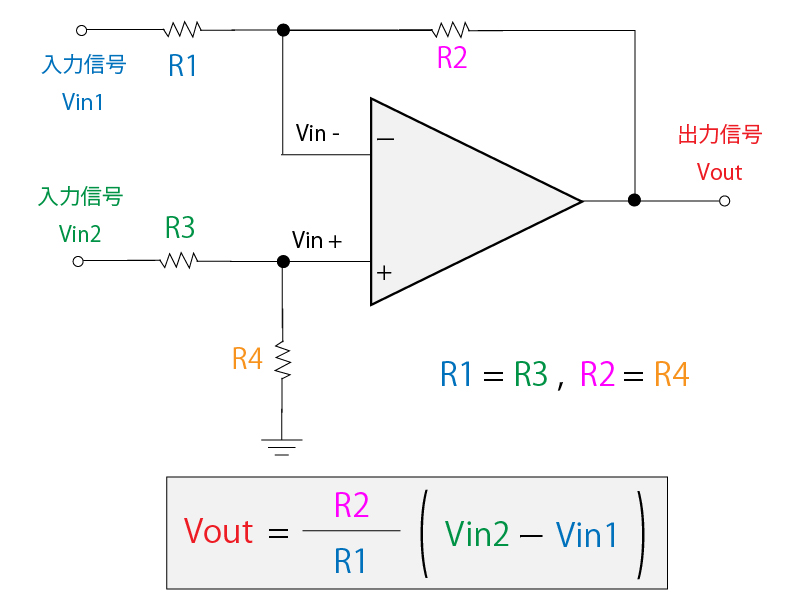
このように、非反転入力端子と反転入力端子の分圧比を等しくすることで、入力信号間の差分だけを取り出して出力することができます。
解析例
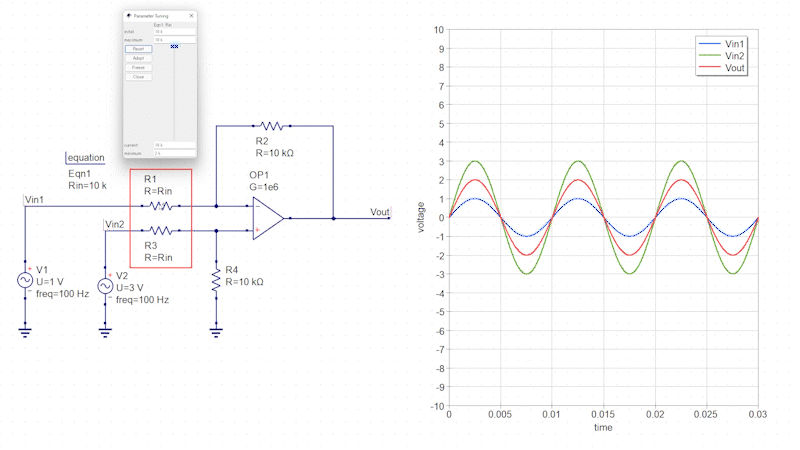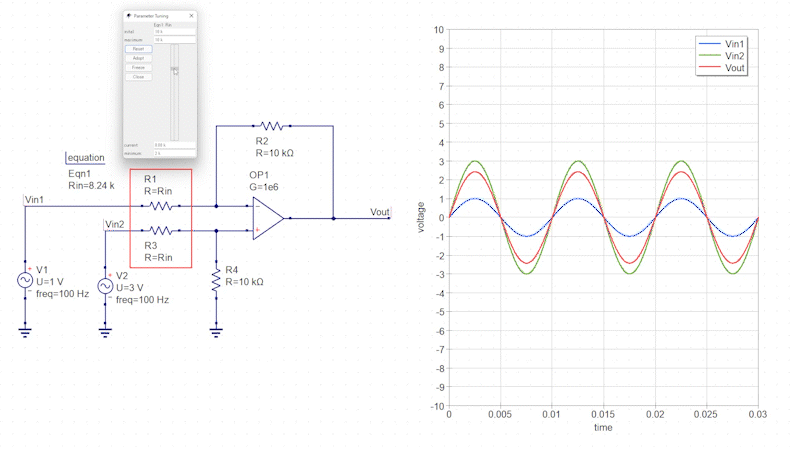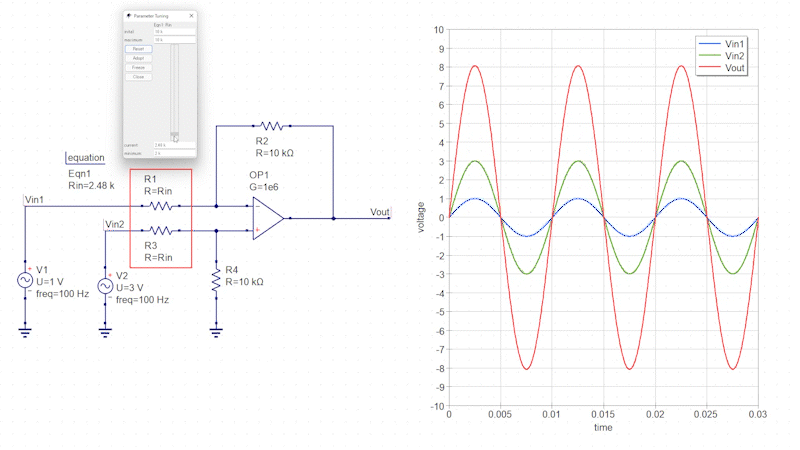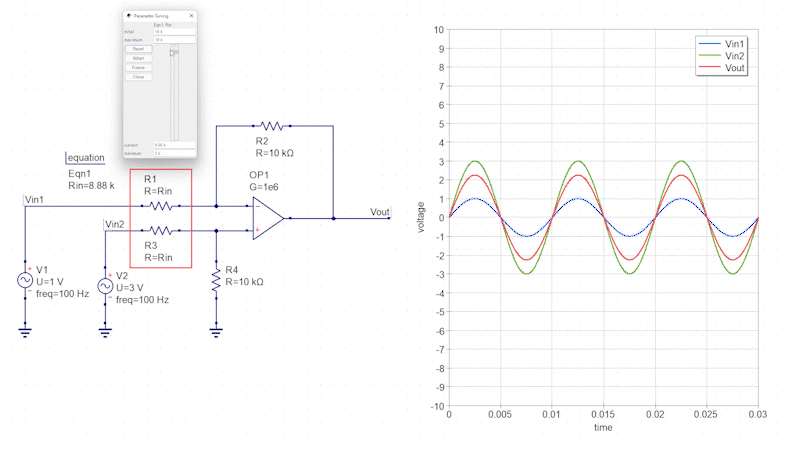
2つの入力信号(V1=1V、V2=5V)を減算回路に接続します。
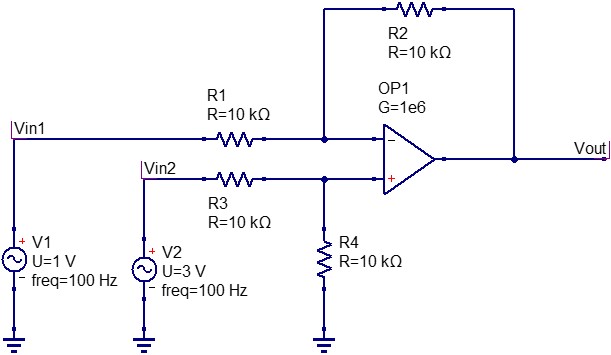
この減算回路では、入力信号の差分信号が出力されます。
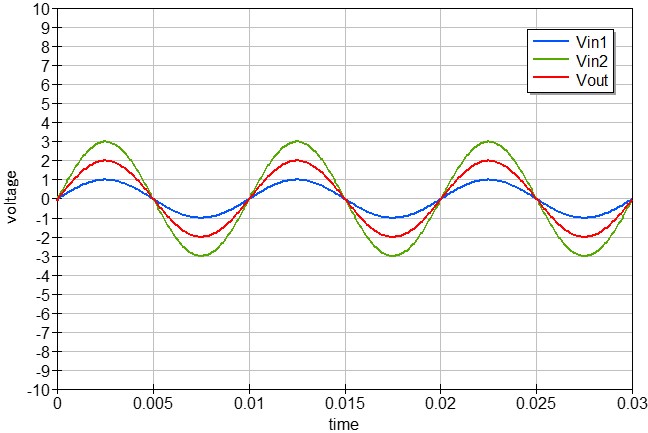
また「R1」と「R3」の抵抗値を変化させることで、差分増幅回路のように増幅率を変化させることも可能です。

微分回路
微分回路は、入力信号の電圧の時間微分する回路で、ハイパスフィルタとして機能する働きを持ちます。
回路構成
微分回路は、反転増幅回路の入力抵抗をコンデンサに置き換えた回路となります。
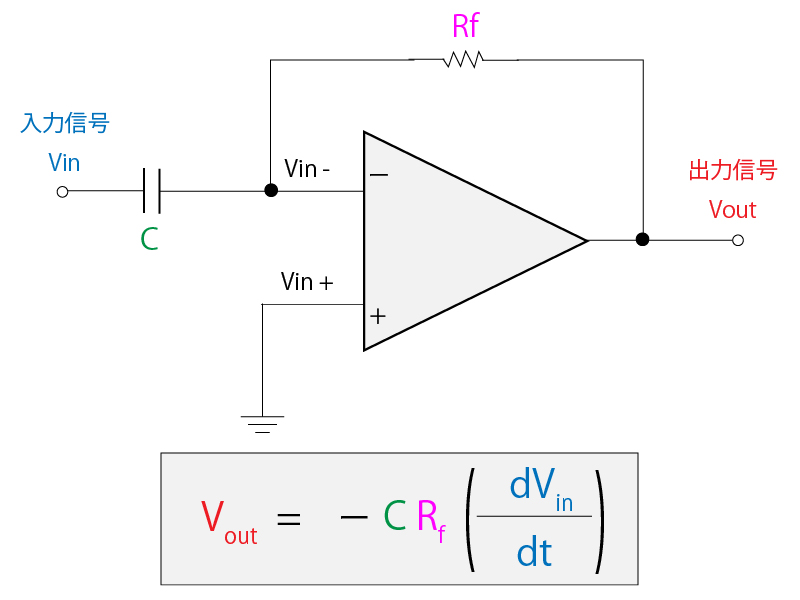
抵抗がコンデンサに置き換わることによって、直流電流(低周波)が流れなくなるためにハイパスフィルタとして作用します。
なお微分回路では、コンデンサのインピーダンスZcと帰還抵抗R2の比によって増幅率が決まりますが、高周波においてはコンデンサのインピーダンスが低くなりすぎて(ゲインが高くなりすぎて)オペアンプが発振します。
そのため、ゲインを制限するための抵抗をコンデンサに直列に接続します。
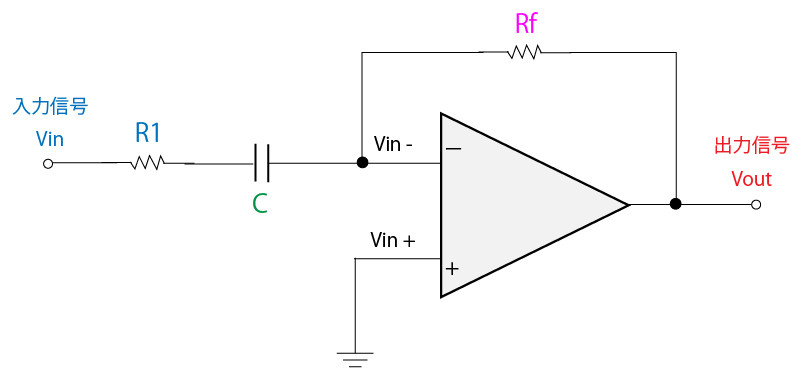
この直列に接続された抵抗によって、コンデンサのインピーダンスが低くなったとしてもゲインが一定以下になるよう制限され、発振を抑制することができます。
解析例
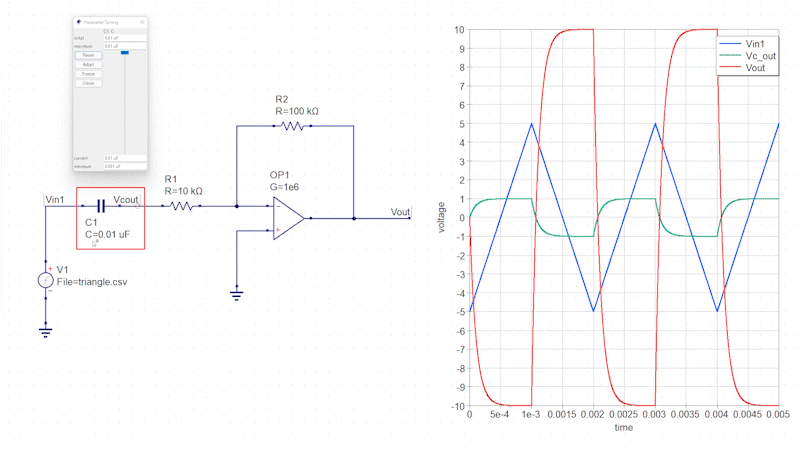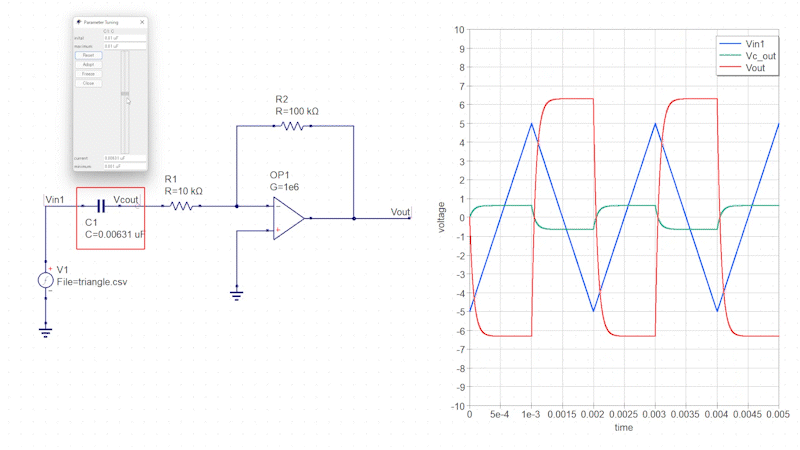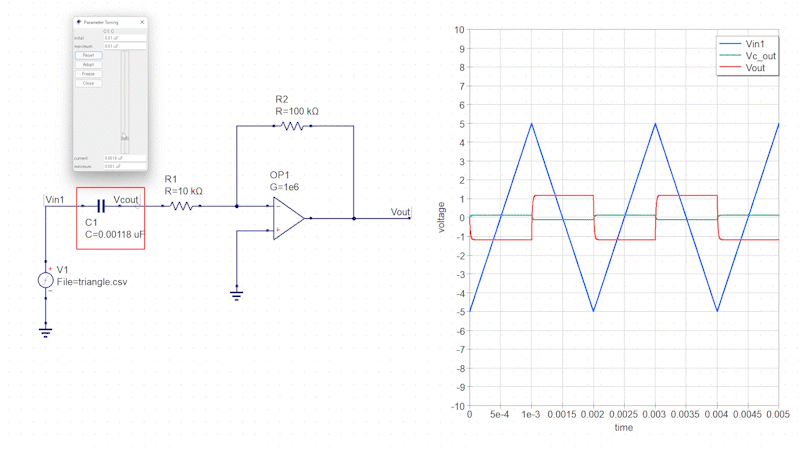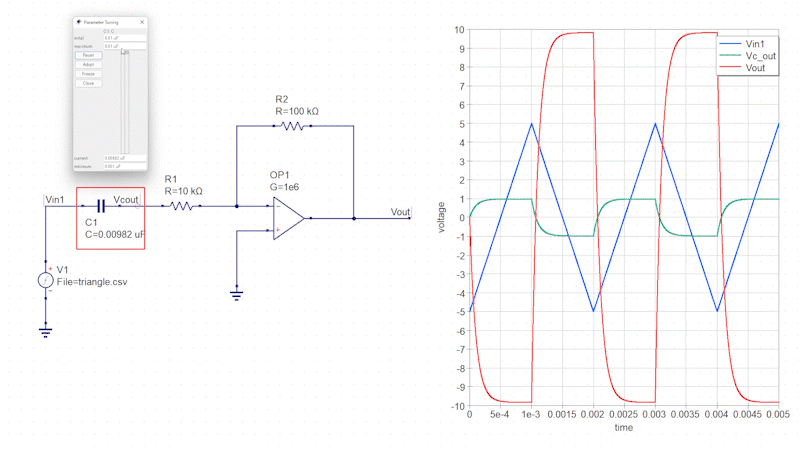
三角波の入力信号を微分回路に接続します。

この微分回路では、入力信号直下のコンデンサによって三角波が矩形波に変化し、その矩形波が反転増幅回路によって増幅されます。
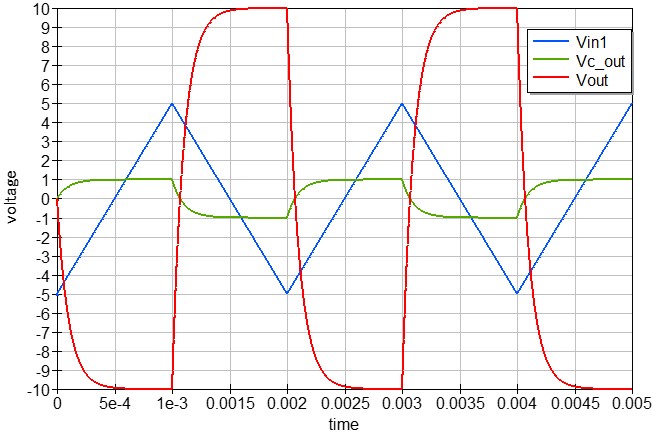
コンデンサの静電容量を変化させるとインピーダンスが変化し、それに伴って出力信号の増幅率も変化します。

積分回路
積分回路は、入力信号の電圧の時間積分する回路で、ローパスフィルタとして機能する働きを持ちます。
回路構成
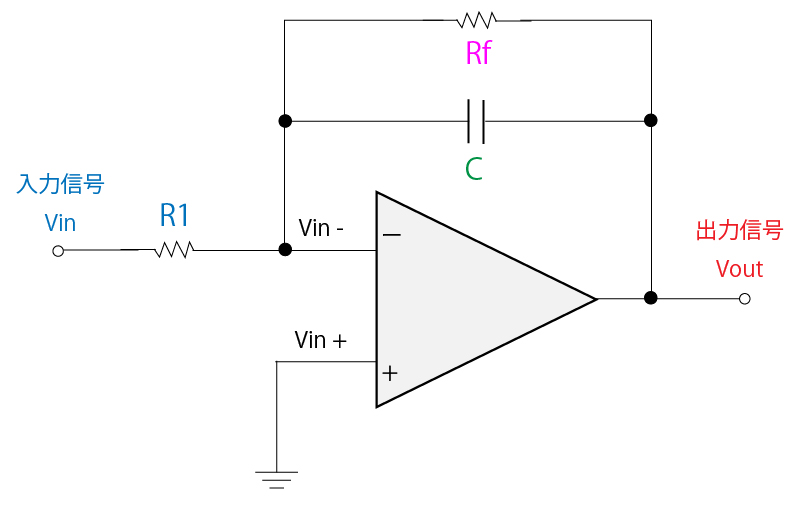
積分回路は、反転増幅回路の帰還抵抗をコンデンサに置き換えた回路となります。
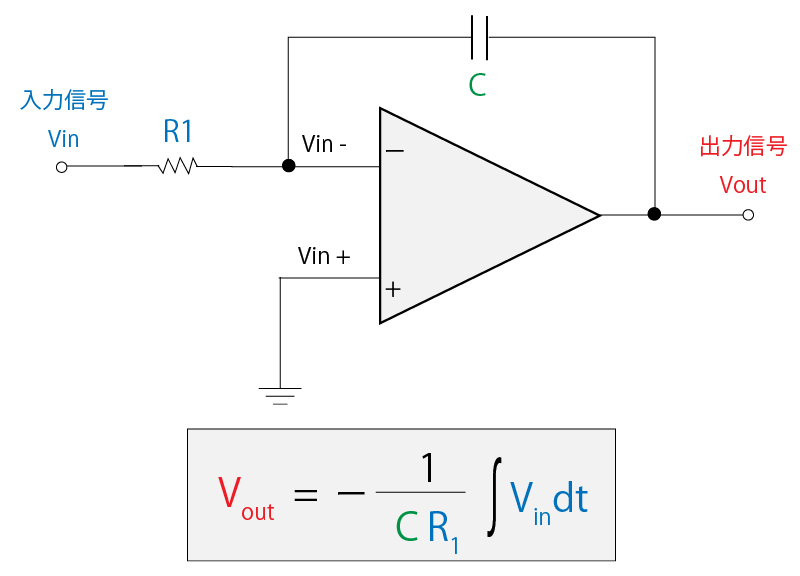
帰還抵抗がコンデンサに置き換わることによって、高周波でのインピーダンスZcが非常に小さくなり、それに伴ってゲイン(G=Zc/R1)も小さくなります。
つまり、高周波をカットするということです。
一方で、低周波においてコンデンサのインピーダンスが高いことで、ゲイン(G=Zc/R1)が高くなりすぎるために、実際の回路においてはコンデンサと並列に帰還抵抗を接続して使用します。
解析例
矩形波の入力信号を積分回路に接続します。
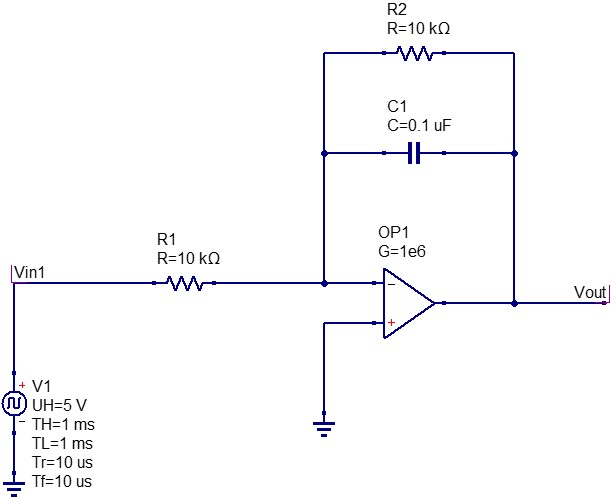
すると、矩形波の「High」と「Low」に応じてコンデンサに充放電電流(三角波)が流れ、その三角波が反転増幅回路によって増幅されます。
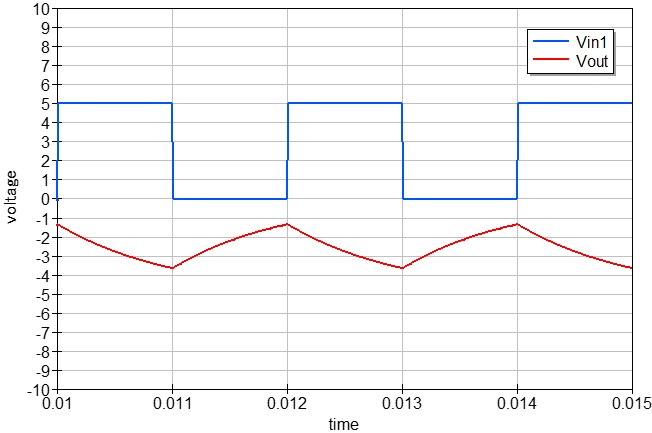
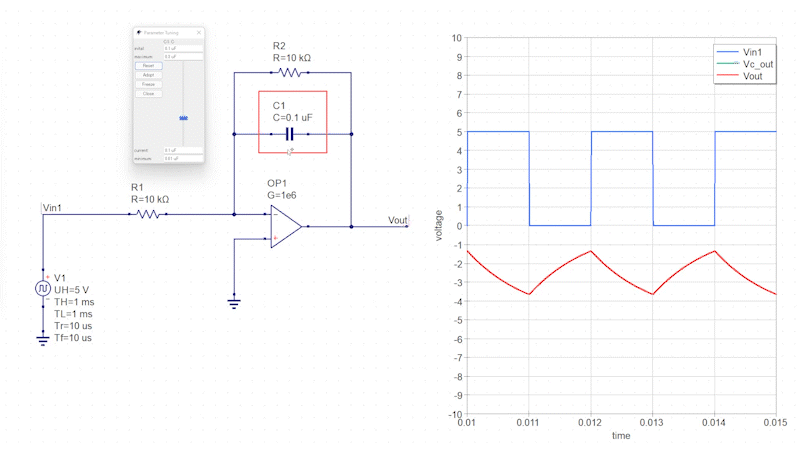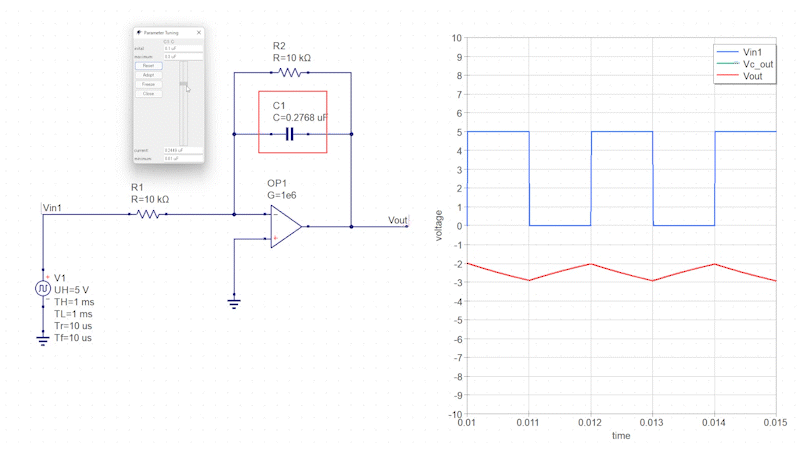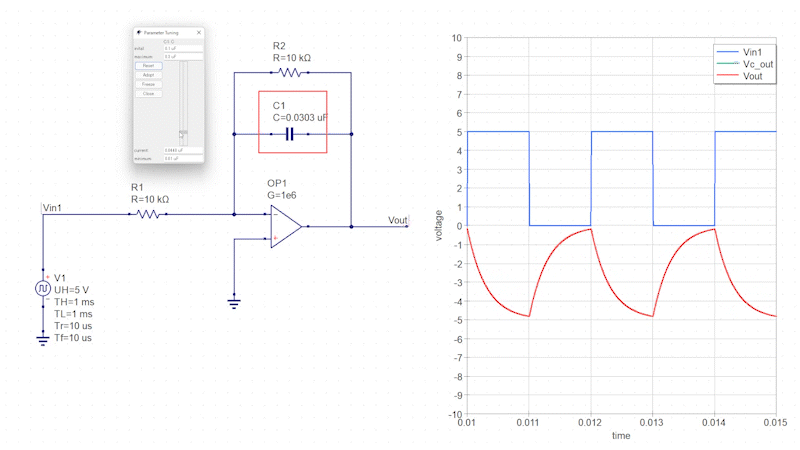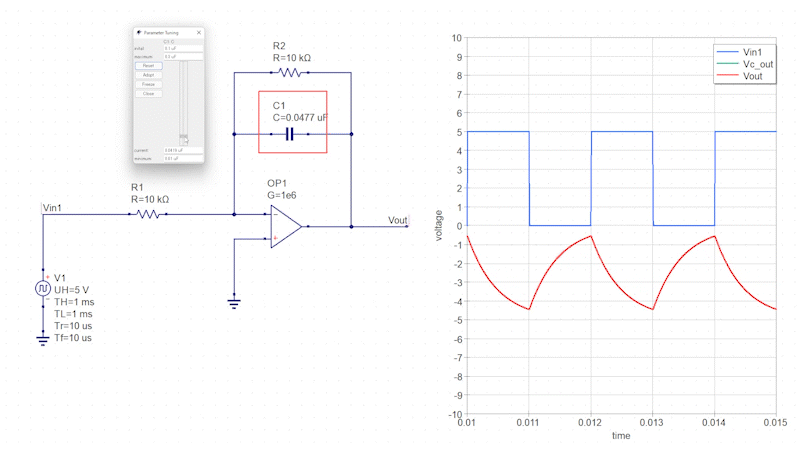
コンデンサの静電容量を変化させるとインピーダンスが変化し、それに伴って出力信号の増幅率も変化します。
おわりに
今回は、オペアンプを使った演算回路を4つ解説しました。
特に微分回路と積分回路は、センサ用のフィルタとして様々な場面で使用するため、回路構成とともに原理をきちんと理解しておくことが大切です。
アクティブフィルタの設計方法については、以下の記事で解説しています。

今回は以上です。
最後まで読んでいただき、ありがとうございました。