伝送線路でインピーダンスマッチング

前回の記事でコイルとコンデンサを使用した「集中定数型」のインピーダンスマッチングの方法を解説しました。

今回は伝送線路のパターンを利用した「分布定数型」のインピーダンスマッチングの方法を解説します。
動画はコチラ↓
分布定数回路とは
分布定数回路は、伝送線路の長さと信号の波長の関係として表されるもので、ここでは集中定数回路との違いをもとにその特徴を見ていきます。
集中定数回路
まず集中定数回路の方は、例えば300mm の伝送線路と周波数が低い信号(10kHz)があったとします。
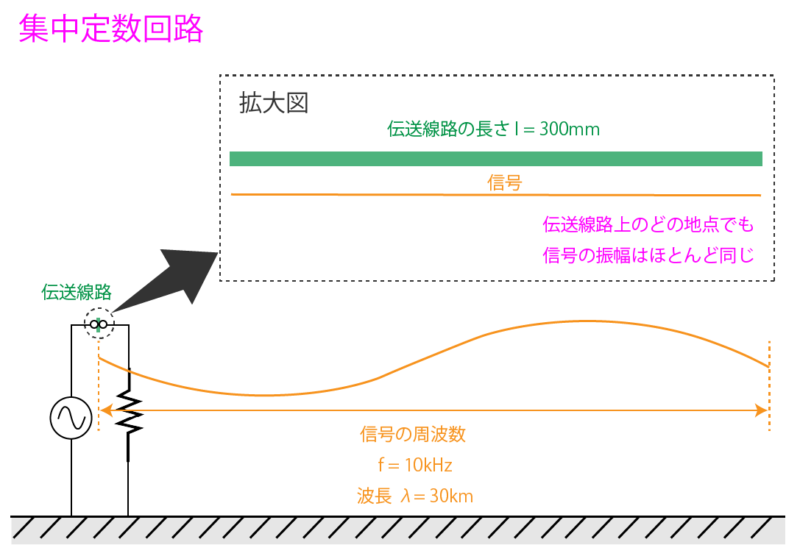
この信号の波長は λ = 30 km と伝送線路の長さ 300 mm に対して波長が非常に長いですよね。
このような場合、伝送線路上を信号が伝搬するときに伝送線路上で信号は位相がほとんど変化しないため、どの箇所でもだいたい同じ振幅となります。
つまり伝送線路全体を単純に一つの線として捉えることができるということです。
分布定数回路
一方、分布定数回路は、同じ伝送線路に対して信号の周波数が 1GHz だったとすると、信号の波長は λ = 300 mm となります。
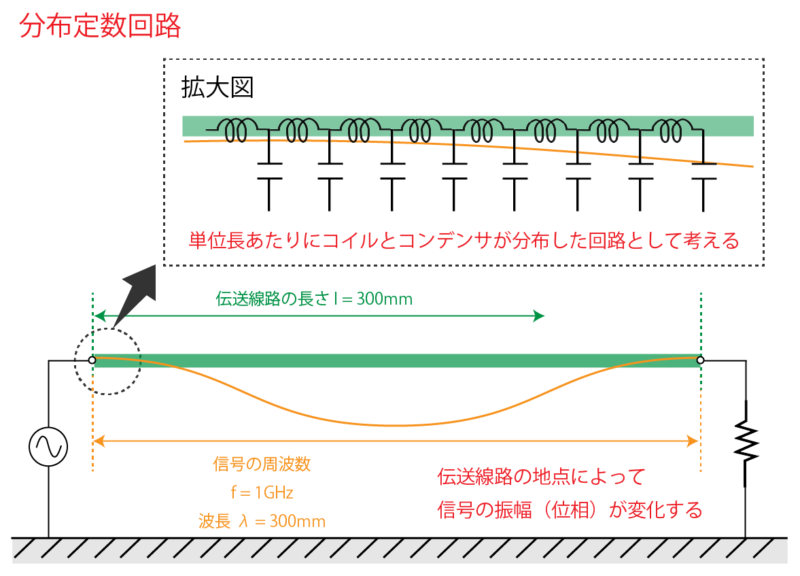
この信号が伝送線路を伝搬する場合には、伝送線路上の場所によって信号の位相が異なるため、場所ごとに振幅が大きく変化します。
このような場合、伝送線路は長さが少し変わっただけで通過する信号の振幅が変わってしまうということで、伝送線路そのものを単純に1つの線として扱うことは難しいです。
そのため、単位長さあたりにコイルとコンデンサが分布した有限長の伝送線路として考える必要があります。
ちなみに、どれくらいの波長から分布定数回路として考えるべきかについては、伝送線路の長さが λ/20 を超えたくらいが1つの目安となります。
この λ/20 というのは、位相が 18° 変化するということを意味しており、正弦波で考えると振幅が最大で 3割ほど変化するということになります。

入力インピーダンスとは
分布定数回路では伝送線路の長さによって振幅が変化しますが、これを別の言い方にすると、伝送線路の長さによってインピーダンスが変化するというように表すことができます。
ここで言うインピーダンスは、回路の入力インピーダンスのことです。
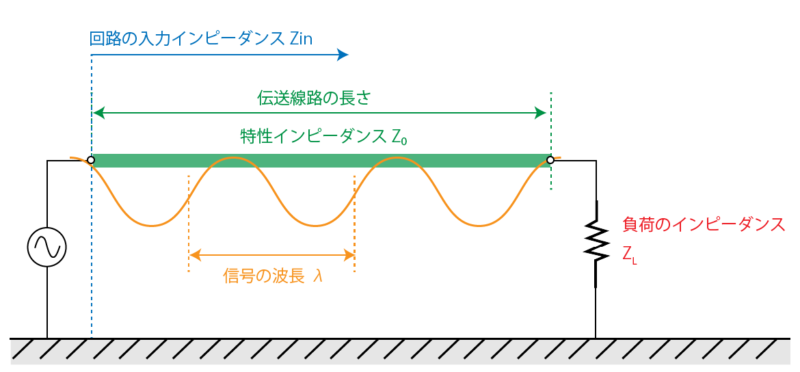
伝送線路を加味したときの回路の入力インピーダンス Zin は
Zin = Z0 * (ZL+jZ0 tanθ) / (Z0+jZL tanθ) で表されます。
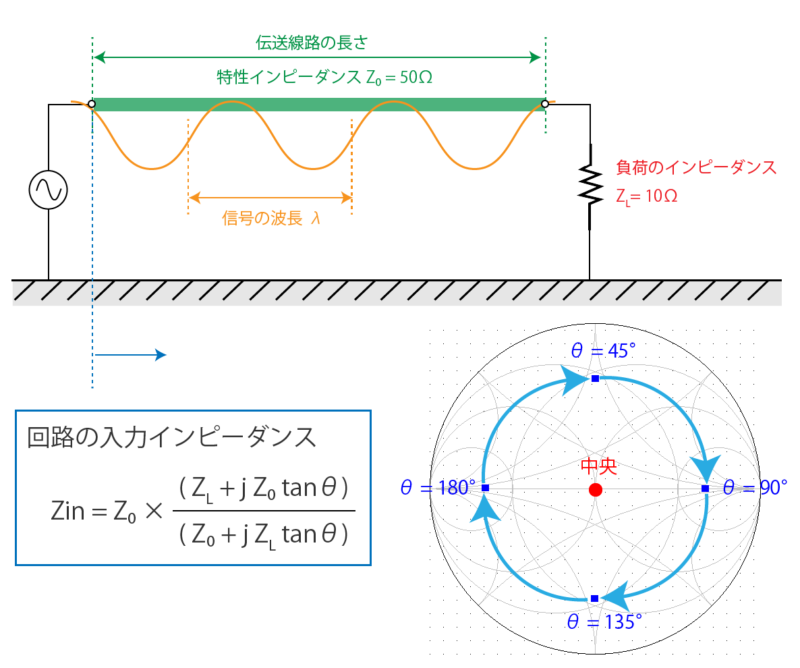
このときに例えば、Z0 = 50Ω、ZL = 10Ω として
θ を 45°、90°、135°、180°と変化させたとすると、それぞれの入力インピーダンスは、スミスチャートの中央から等距離を守ったまま、時計回りにその特性が変化していきます。
このように分布定数回路においては、伝送線路を挿入するだけで回路の入力インピーダンスが変化します。

インピーダンスマッチングの方法
実際に伝送線路を使ってインピーダンスマッチングしてみます。
ここで気をつけるべきポイントは以下の2点です。
- Zin の「虚数部」が消えるように「伝送線路の長さ」を調整する
- Zin が 50Ωとなるように「伝送線路の特性インピーダンス」を調整する
ここでは負荷のインピーダンス ZL を 10Ω 、インピーダンスマッチングの対象となる周波数を 1GHz として考えます。
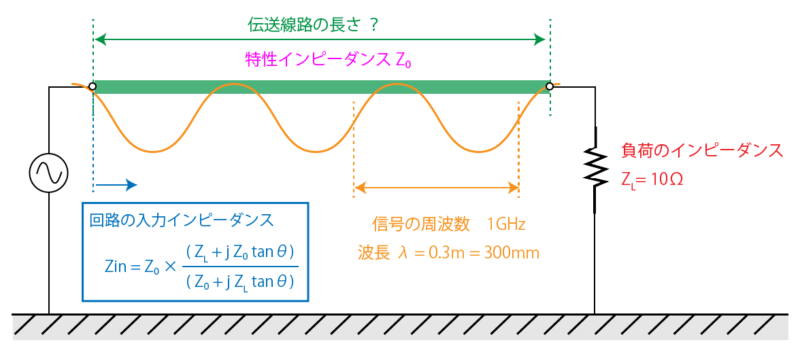
まずは①の虚数部が消えるための条件を考えます。
最も単純なのは θ = 0 のときですが、これでは伝送線路がないことになるのでここでは除外します。
次に出てくるのが θ = 90° のとき、つまりは伝送線路の長さが波長に対して λ/4(7.5mm)のときです。
このときの入力インピーダンスは、分母と分子をそれぞれ tan(λ/4) = ∞ で割ると
Zin = Z0^2 / ZL となり
これで虚数部を消すことができます。
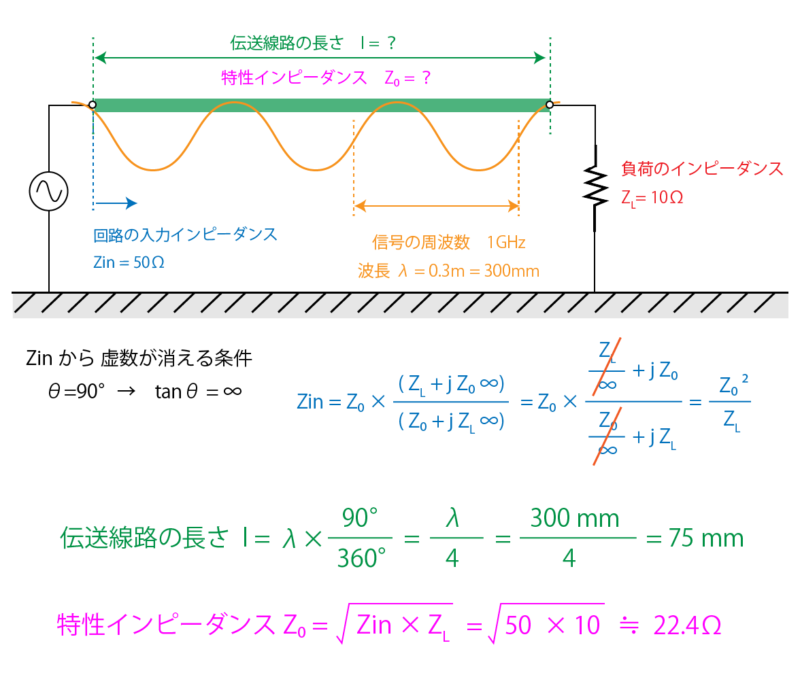
そして次は②の伝送線路の特性インピーダンスを求めたいので、入力インピーダンスの式を変形して
Z0 = √Zin * ZL とし
ここに、回路の入力インピーダンス Zin = 50Ω と負荷のインピーダンス ZL = 10Ω を代入します。
すると伝送線路の特性インピーダンスは、Z0 = 22.4 Ω ということになります。
つまり負荷のインピーダンスが 10Ωの場合には、伝送線路が波長に対して λ/4 の長さを持ち、かつ特性インピーダンスが 22.4Ω のときにインピーダンスマッチングできるということになります。
実際に回路シミュレータを使ってその特性を確認してみると、インピーダンスマッチングできています。
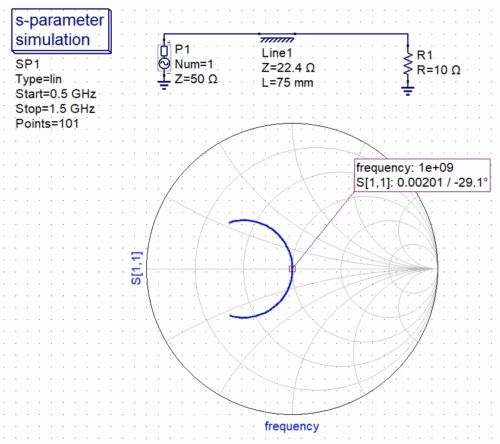
このように波長に対して 伝送線路の長さを λ/4 とするインピーダンスマッチング回路のことを「λ/4 変成器」と呼びます。
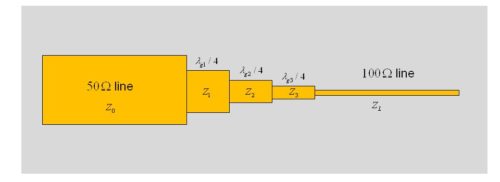
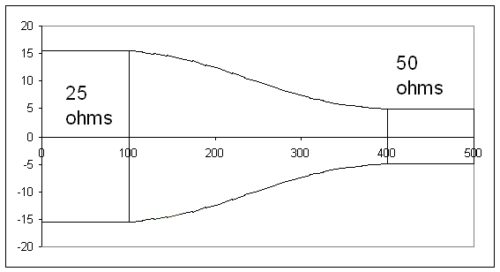
実際の回路では、マッチングの帯域を広げるためにλ/4 変成器を多段に接続したものや、テーパー状にして連続的にインピーダンスを変化させたものが使われています。

おわりに
今回は伝送線路のパターンを利用した分布定数型のインピーダンスマッチングの方法を紹介しました。
分布定数回路は、高周波の回路に馴染みがない方にとっては難しそうな印象を受けるかもしれませんが、計算そのものはコンピュータで処理することがほとんどです。
そのためまずは回路シミュレータなどを使って基礎をきちんと理解し、そこから応用を学習していくと良いかと思います。
高周波回路においては、座学だけではなかなか理解が難しいのが実情です。
一方で実務だけでも現場でのテクニックは身につくものの、本質的な理解を得ることはなかなか難しいです。
そのためレベルアップを図るには座学と実務のバランスが重要となるわけですが、そのような観点で見たときにオススメできるのが「高周波回路の設計と製作」です。
(2026/02/21 12:11:14時点 Amazon調べ-詳細)
この書籍は、高周波でよく使用する回路や部品の原理が数式をもとにして解説されていることに加えて、原理の正しさや意味を回路シミュレータを使って自身で検証できる内容となっています。
まさに座学と実務をバランスよく学べる内容です。
それぞれの回路に関連した専門用語も適宜説明されているので、高周波回路をこれから学んでいくという方にはピッタリの内容かと思います。
高周波用の回路シミュレータとしては「QucsStudio」がおすすめです。
今回は以上です。
最後まで読んでいただき、ありがとうございました。