トロイダルコイルの設計方法

コイルの特性として最も重要なパラメータは「インダクタンス」ですが、インダクタンスはコイルの形状によって計算方法が異なります。
そこで今回の記事では、磁性体を使ったコイルとして最もベーシックな「トロイダルコイル」の設計方法について紹介します。
動画はコチラ↓
インダクタンスの計算方法
トロイダルコイルのインダクタンスは、数に記載されている式から計算できます。
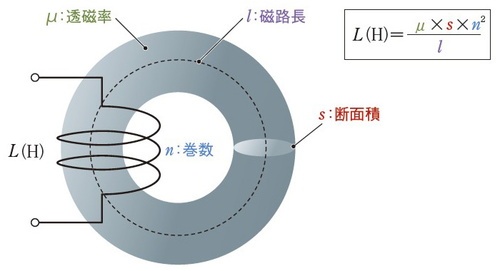 トロイダルコイルのインダクタンス 出典:日経XTECH
トロイダルコイルのインダクタンス 出典:日経XTECHこの式に基づくと、トロイダルコアの透磁率 μ 、磁路長 l 、断面積 S 、コイルの巻数 N をもとにコイルのインダクタンスが求まります。
では、この式がどのように導出されるかを考えてみましょう。

トロイダルコイルとは
そもそもトロイダルコイルとは、トロイダル状のコアにコイル(電線)を巻いたものです。
主に電源ライン用のコモンモードチョークコイルなどに使用されています。
 コモンモードチョークコイル 出典:Wurth Electronics
コモンモードチョークコイル 出典:Wurth Electronicsトロイダルコイルの特徴は、磁束がすべて磁性体中を通る「閉磁路」で、かつ磁界の発生方向(右ねじの法則)と同じ形状であるため、効率的に磁界を取り込むことが挙げられます。
そのため、コイルとして最も性能が良い形状と言えます。


磁気回路とは
コイルを設計する場合には、「磁気回路」で考えます。
電気回路では「オームの法則」があり、電圧E、電流I、抵抗Rとすると、以下の式になりますね。
E = I * R ・・・①
磁気回路にもオームの法則に相当する公式が存在します。
- 「電圧 E」⇛「起磁力 Fm」
- 「電流 I」⇛「磁束 Φ」
- 「抵抗 R」⇛「磁気抵抗 Rm」
よって磁気回路におけるオームの法則は以下の式になります。
Fm = Φ * Rm ・・・②
【単位】
- 起磁力Fm 【AT(アンペアターン)】コイルの巻数と電流の積
- 磁束Φ 【wb(ウェーバー)】
- 磁気抵抗Rm【AT/wb】
磁気抵抗の導出
ここでトロイダルコイルの磁気抵抗 Rm は、磁路長 l と断面積 S から求まります。
Rm = l / (μ * S) ・・・③
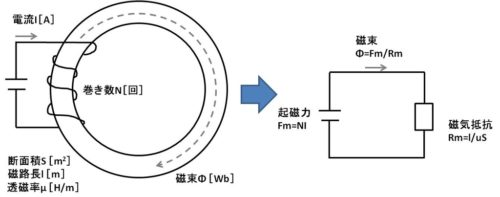 磁気回路 出典:ジャズとエンジニア
磁気回路 出典:ジャズとエンジニアさて、これでインダクタンスを計算する準備が整いました。

インダクタンスの導出方法
トロイダルコイルは、閉磁路であるためコア内のどの位置にも均一な磁界がかかります。
そのため磁気回路の計算ができていれば、インダクタンス L は容易に求まります。
まず式②より、磁束Φを以下のように変形します。
Φ = Fm / Rm
そして起磁力Fm は、コイルの巻数と電流の積によって表されるため、以下の式に変形することができます。
Φ = (N * I) / Rm ・・・④
インダクタンスとは
ここでインダクタンスの定義を確認しておきましょう。
Wikipediaによると
回路に電流が流れると周囲に磁場が形成される。
巻線に電流 I が流れるときの巻線を貫く磁束 Φ であるときの比例係数 L がインダクタンスである。
電流に対して発生する磁束の比例係数がインダクタンスということで、以下のように表されます。
L(インダクタンス) = 鎖交磁束数 ∮ / 電流 I
ここで鎖交磁束数∮と磁束Φの関係は以下の式で表されます。
∮ = N * Φ
インダクタンスの導出
よって、インダクタンスは以下のように求まります。
L = (N * Φ) / I
= N^2 / Rm
= (N^2 * μ * S) / l
これで冒頭の計算式に到達しましたね。
 トロイダルコイルのインダクタンス 出典:日経XTECH
トロイダルコイルのインダクタンス 出典:日経XTECH
おわりに
磁気回路は毛嫌いしがちですが、そんなに難しい計算をしているわけではありません。
オームの法則が理解できていれば、誰でも計算可能です。
トロイダルコイルはその中でも最も計算が容易なので、例えばノイズフィルタ用のコモンモードチョークコイルを計算する場合などで使用してみてください。
コイルの設計方法については【トロイダル・コア活用百科】が非常に参考になります。
(2026/03/08 12:24:29時点 Amazon調べ-詳細)
空芯コイルの設計方法はコチラ
今回は以上です。
最後まで読んでいただき、ありがとうございました。











E = I * Rは、電力式の間違いじゃないでしょうか?
電気式では、E = I ・ R
電気回路では「オームの法則」があり、電圧E、電流I、抵抗Rとすると、以下の式になりますね。
E = I * R ・・・①