スミスチャートとは
スミスチャートは、高周波回路のインピーダンスマッチングに使用される一種のグラフツールで、高周波回路の設計においては無くてはならないものとなっています。
今回はそんなスミスチャートの「概要」とそれに関連した「アドミタンスチャート」や「イミッタンスチャート」について解説します。
動画はコチラ↓
スミスチャートとは
スミスチャートは、一見すると非常に難しそうに見えますが、どのようなものかを理解できていれば実は非常に便利です。

そもそもスミスチャートは、インピーダンスマッチングするのためのグラフツールということで、インピーダンスのグラフを変形したものとなっています。
インピーダンスの図とスミスチャートの図を並べながらそれぞれの関係性を見ていきます。
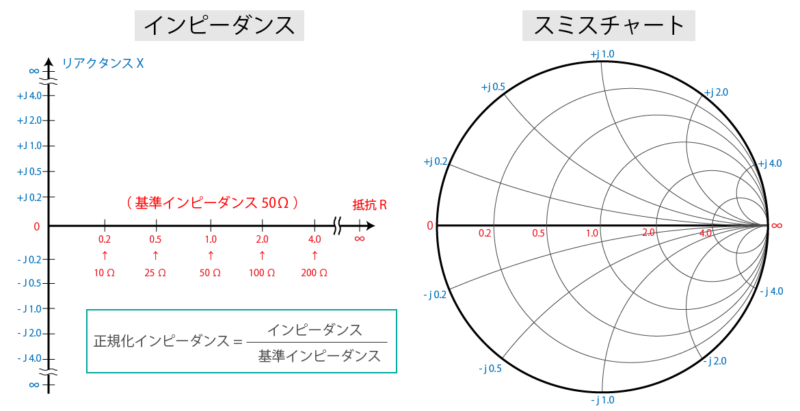
まずスミスチャートで表すにあたって、インピーダンスは通常のインピーダンスではなく
正規化されたインピーダンスとする必要があります。
高周波回路では多くの場合、回路の特性インピーダンスを 50Ωで設計するので、ここでは50Ωを基準として正規化します。
するとインピーダンスの図においては、50Ωが 基準となる 1 、5Ωは 0.1、10Ωは 0.2、100Ωは 2、1000Ωは 20 というに値が変化します。
等レジスタンス円
ここで抵抗が 100Ωとして、リアクタンスの大きさを -∞ ~ ∞ に変化させたとします。
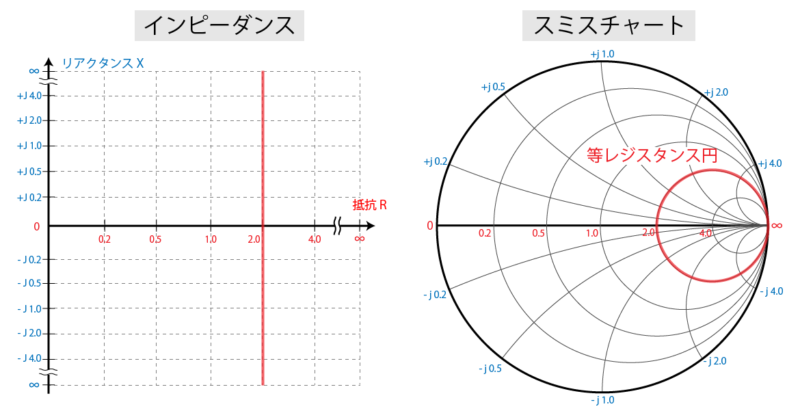
するとその特性は、インピーダンスの図においては抵抗が 2 の位置にまっすぐの直線が引かれるのに対して、スミスチャートでは右端の ∞ から 2 を通る円がプロットされます。
インピーダンスの図では縦一直線だった特性が、スミスチャートでは円状の特性を描くということで、この円を「等レジスタンス円」と呼びます。
スミスチャートでは、この等レジスタンス円が何重にも渡って描かれていますが、これらの円は円上の点がすべて同じ抵抗値であるということを意味しています。
等リアクタンス円
次にリアクタンスを一定としたときのそれぞれの図の違いを見てみます。
ここではリアクタンスの大きさを +j100 Ω として、抵抗値を0 ~ ∞ に変化させます。
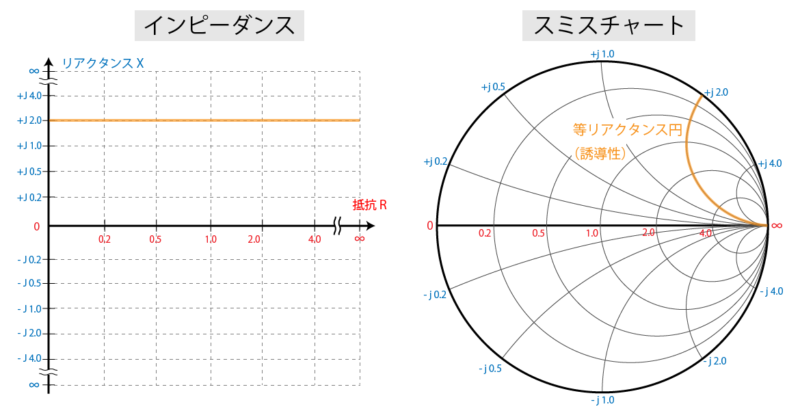
インピーダンスの図においては、リアクタンスが +j2 の位置で横方向にまっすぐの直線が引かれます。
一方スミスチャートでは、抵抗が ∞ のときは右端の位置にプロットされ、そこから抵抗値が小さくなるに従って時計回りに円状の特性が描かれます。
ここではリアクタンスを一定としているので、この円を「等リアクタンス円」と呼びます。
さらにリアクタンスはマイナスの値を取ることが可能です。
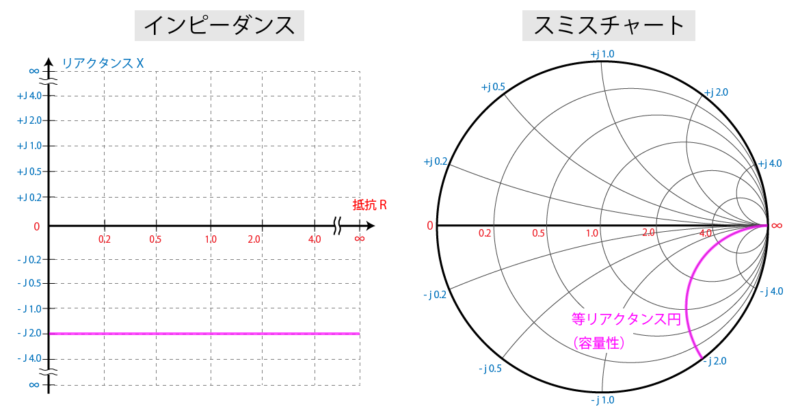
リアクタンスが -j100 Ωで、抵抗値を 0 ~ ∞ に変化させたとすると、スミスチャートでは右端の ∞ から反時計回りにその特性が描かれます。
これも同じく等リアクタンス円ですが、リアクタンスの正負は、それぞれ誘導性のリアクタンスと容量性のリアクタンスを意味していることになります。
インピーダンスマッチング
インピーダンスマッチングをする場合には、コイルとコンデンサを使って等レジスタンス円の円上を移動します。
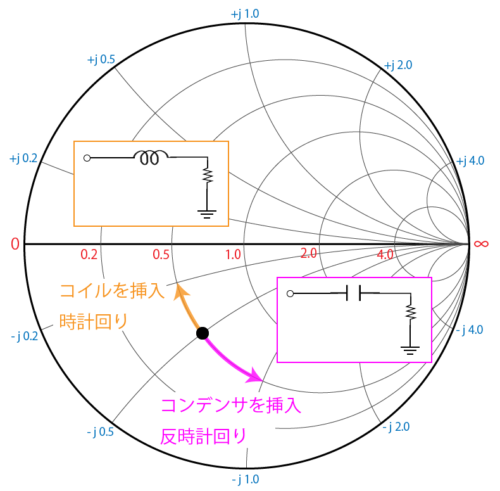
移動するというのはインピーダンスが変化しているということですね。
このようにコイルとコンデンサを使って特定のインピーダンスに移動するというのが、スミスチャートを使ったインピーダンスマッチングの考え方になります。

アドミタンスチャートとは
実際の回路では、スミスチャートだけでインピーダンスマッチングすること難しいです。
それはなぜかと言うと、スミスチャートはあくまでも回路に対して直列にコイルやコンデンサを接続するときに使うものですが、実際の回路では並列に接続することもあるためです。
アドミタンス
コイルとコンデンサは並列に接続した場合には、計算を簡単にするためインピーダンスの逆数をとったアドミタンスとして特性を表します。

アドミタンスは電流の流れやすさを表しており、単位は S 「ジーメンス」で表されます。
このアドミタンスはインピーダンスの逆数なので
アドミタンス Y = 1/R + 1/jwL + jwC となり
このうち抵抗に関わる 1/R をコンダクタンス G、リアクタンスに関わる 1/jwL と jwC をサセプタンス B と呼びます。
アドミタンス Y = G + jB としても表されることもあります。
アドミタンスチャート
回路に並列に接続した場合には、アドミタンスチャートを使ってインピーダンスマッチングを行います。

アドミタンスチャートは、図としてはスミスチャートを左右反転した形で、左端が ∞ [S]、右端が 0 [S] となっています。
そして左端から描かれている円が「等コンダクタンス円」、上下に円の一部が描かれているのが「等サセプタンス円」となります。
等コンダクタンス円は、位置づけとしてはスミスチャートにおける等レジスタンス円と同じものになります。
等サセプタンス円は、正の値のときはコンデンサとしての性質、負の値のときはコイルとしての性質を持ちます。
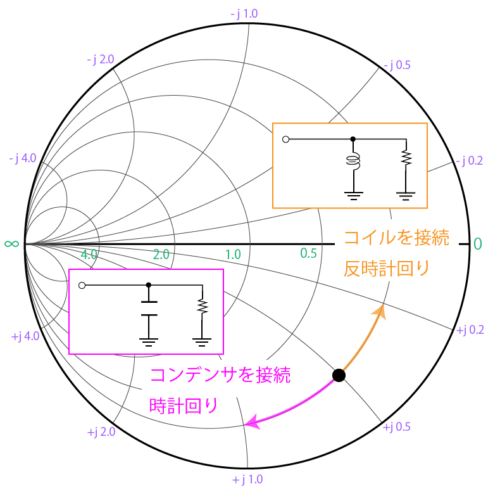
そのため、回路に対して並列にコンデンサを接続すると等コンダクタンス円上を時計回り、コイルを接続すると反時計回りに移動することができます。
このようにアドミタンスチャートを使用することで、並列回路に対応したインピーダンスマッチングも行えるようになります。

イミッタンスチャートとは
実際の回路では、直列回路と並列回路を組み合わせてインピーダンスマッチングするということで、チャートの方もスミスチャートとアドミタンスチャートを組み合わせた「イミッタンスチャート」が使われます。
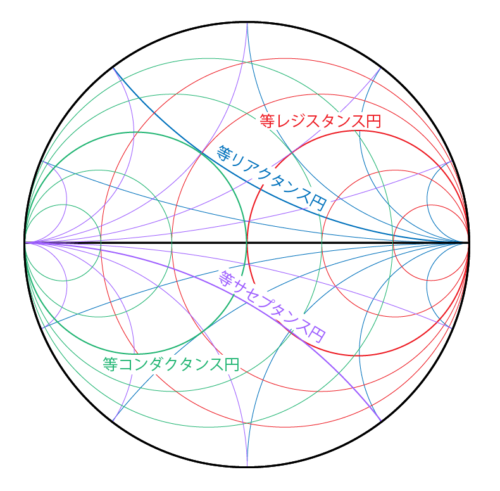
イミッタンスチャートは、スミスチャートの「等レジスタンス円」と「等リアクタンス円」さらにはアドミタンスチャートの「等コンダクタンス円」と「等サセプタンス円」が重なり合うように図示されています。
この図だけ見ると難しそうに見えるかもしれませんが、それぞれの線はこれまで説明してきた円の重なりに過ぎないので、使い方さえわかってしまえばそれほど難しくないはずです。

インピーダンスマッチングの例
ここでは「Quick Smith」 というWeb上のアプリケーションを使って、50Ωの伝送線路と 75Ωの負荷のインピーダンスマッチングの方法を解説します。
入力インピーダンス Zin = 75 Ωとすると、正規化インピーダンスが 1.5 となるため、イミッタンスチャート上の1.5 + j0 の位置に青い点がプロットされます。
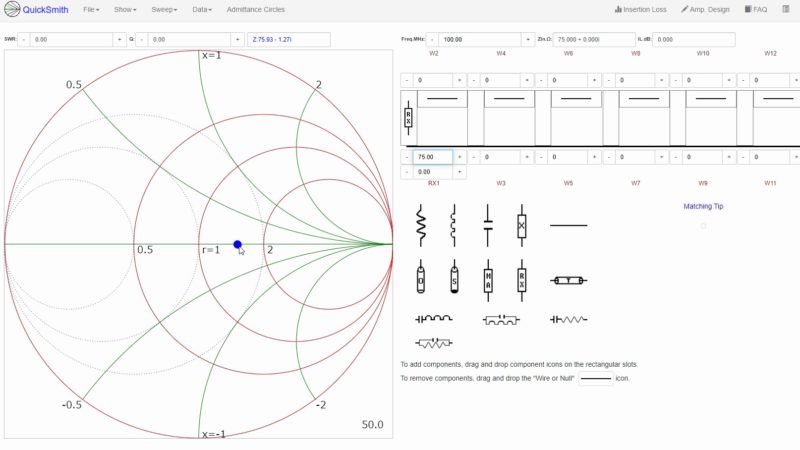
ここから等レジスタンス円や等コンダクタンス円を使って r = 1 + j0 の位置に移動すればいいので、今回は等コンダクタンス円を時計回りに移動し、そこから等レジスタンス円を時計回りして r = 1 + j0 の位置に移動します。
等コンダクタンス円を時計回りするには並列にコンデンサを接続すればいいので、まずは回路に並列にコンデンサを追加します。
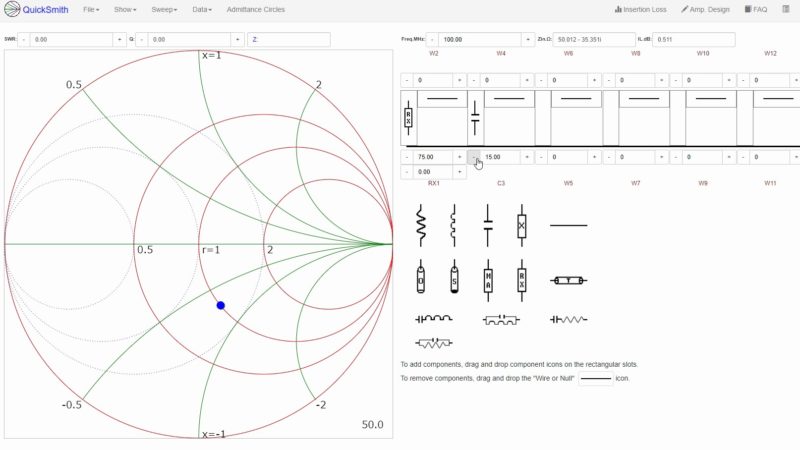
定数は r=1 の等レジスタンス円に重なるよう調整します。
次に等レジスタンス円を時計回りするので、コイルを直列に接続します。

ここでは r = 1 + j0 の点に近づくようコイルの定数を調整します。
そして青い点が r = 1 + j0 に移動したところで、インピーダンスマッチングは完了です。
今回の例では、負荷に対して並列に 15 pF のコンデンサが接続され、さらにその手前側に直列に56 nH のコイルが接続される結果となりました。
おわりに
今回はスミスチャートの概要とそれに関連してアドミタンスチャートとイミッタンスチャートについて解説しました。
実際の設計においては、直列回路と並列回路の両方に対応したイミッタンスチャートを使ってインピーダンスマッチングを行います。
最後に使用した「Quick Smith」 は、スミスチャートがどのようなものかを学ぶにはうってつけのツールです。
誰でも無料で使えるので、ぜひ一度使ってみて、手を動かしながらスミスチャートについて学んでみてください。
Quick Smith の使用例はコチラ↓

今回は以上です。
最後まで読んでいただき、ありがとうございました。