オームの法則の基本
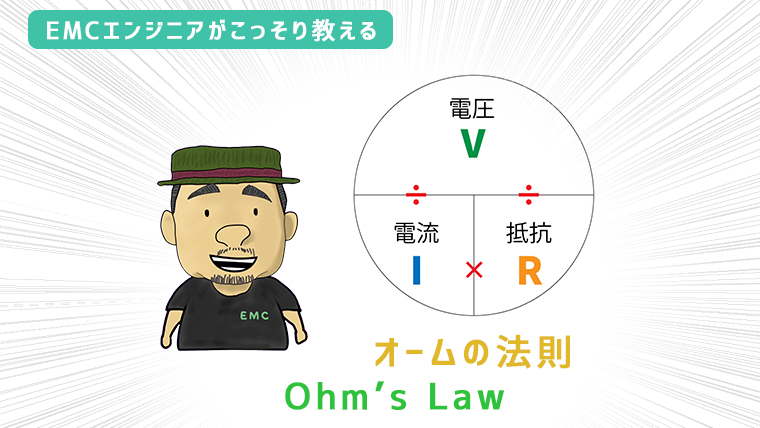
オームの法則は、電気回路の最も基本的な法則です。
そこで今回の記事では、実務レベルにおけるオームの法則の「概要」と「直列回路」「並列回路」それぞれの回路での要点について解説します。
オームの法則とは
オームの法則は、直流回路における「電圧」「電流」「抵抗」の関係性を表したものです。
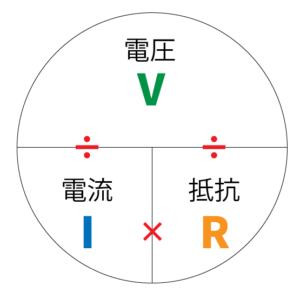
オームの法則においては、2点間の電位差(電圧)とそこに流れる電流は、比例定数(抵抗)をもとに V=IR として表されます。
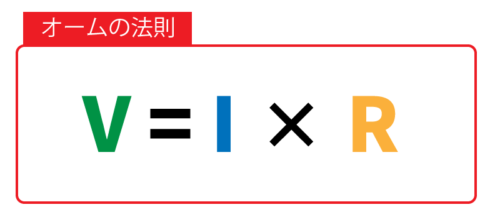
このオームの法則は、実務における様々なシーンで活用されています。
抵抗とは
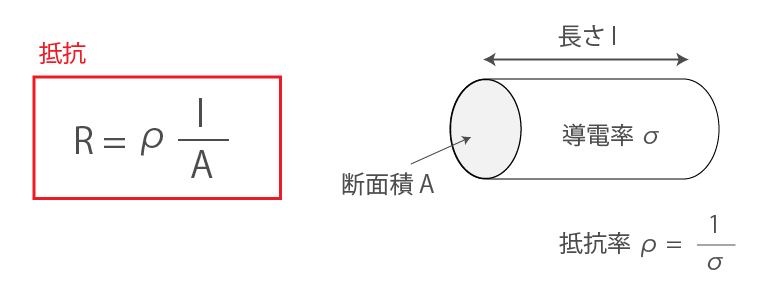
ここでの抵抗は電気の流れにくさのことで、単位は「Ω:オーム」で表されます。
導体の抵抗は、長さが l 、断面積が A すると、電気の流れやすさを表す「導電率σ」とその逆数の「電気抵抗率 ρ」をもとにして求めることができます。
交流回路
交流においては、「抵抗R」が「インピーダンスZ」に変化します。

ただし、インピーダンスに変化したからといって、電圧と電流の関係を表すという、その本質が変化するわけではありません。
インピーダンスの詳細はこちら↓

そのため交流回路まで含めると、電気回路のうちの半分以上はオームの法則だけで回路の役割を説明することが可能です。

直列回路
話を直流に戻して、ここでは直列回路におけるオームの法則について考えてみます。
直列回路は、抵抗が複数個、同一線上に並んだ回路です。
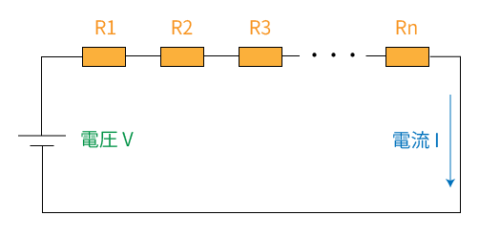
直列回路の特徴としては
- 回路の合成抵抗は、各抵抗の和 R=R1+R2+・・・+Rn
- 合成抵抗とオームの法則から、回路中に流れる電流 I = V/R が求まる
- 回路中のどの箇所とも電流値は一定
- 各抵抗に掛かる電圧は Vx = I✕Rx で求まる
具体例
例えば12Vの電圧源に対して、2Ω、4Ω、6Ωの抵抗を直列に接続したとします。
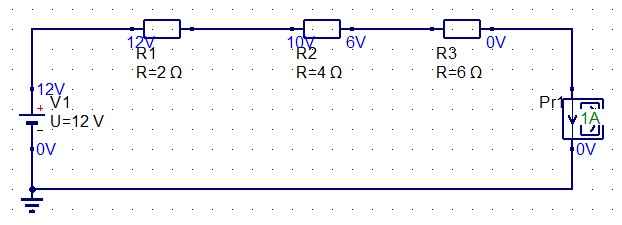
すると合成抵抗は12Ωとなるため、回路中に流れる電流は I=V/R より 1Aと求まります。
また各抵抗に掛かる電圧は、2Ωの場合 V1=1A✕2Ω = 2V となり、その他の抵抗に関しても同様の手順で電圧を求めることができます。
ちなみに、抵抗による電圧降下の和と電源電圧は必ず等しくなり、これをキルヒホッフの法則の第2法則と呼びます。(意味は重要ですが、用語は覚える必要はありません)

並列回路
並列回路は、抵抗が複数個、横並びになった回路です。
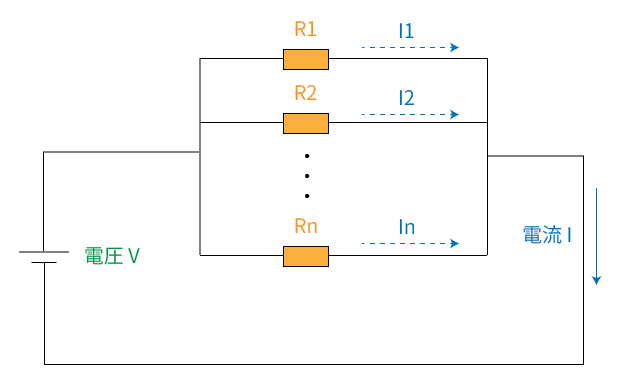
並列回路の特徴としては
- すべての抵抗に同じ電圧 V が掛かる
- 各抵抗に流れる電流は Ix=V/Rx で求まる
- 各抵抗に流れる電流の総和が、回路全体の電流値となる I=I1+I2+・・・+In
- 合成抵抗は R=V/I で求まる
ただし1点補足として、合成抵抗は別の式からも求めることができます。
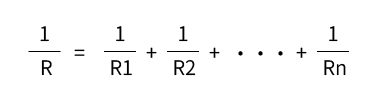
そして上式は、2並列の回路の場合には簡略化することができます。
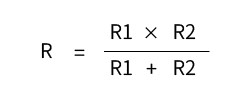
この式は、分母に抵抗の「和」、分子に抵抗の「積」をとった形となっているため「和分の積」と呼ばれており、実務においても重宝する公式です。
具体例
12Vの電源に対して、2Ω、4Ω、6Ωの抵抗を並列に接続したとします。
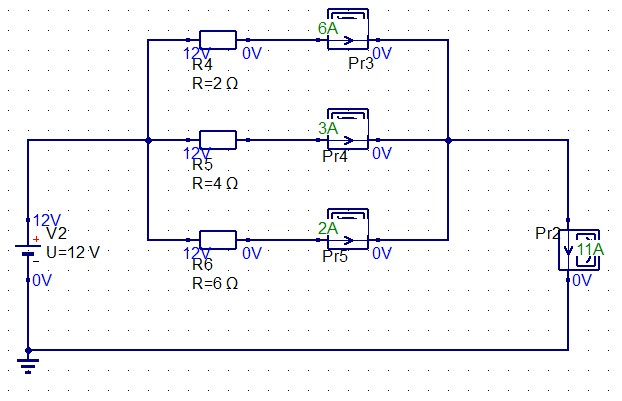
すると各抵抗には12Vの電圧が掛かるため、オームの法則 I=V/Rx に基づいて 6A、3A、2Aの電流が流れ、回路全体にはそれらの和の 11Aの電流が流れます。
そして合成抵抗は R=12V/11A ≒ 1.1Ω と求まります。
ちなみに分岐点において、流入する電流の和と流出する電流の和は必ず等しくなり、これをキルヒホッフの法則の第1法則と呼びます。(意味は重要ですが、用語は覚える必要はありません)

おわりに
今回はオームの法則の概要と、直列回路・並列回路の計算方法について解説しました。
具体例で示したように、抵抗の直列回路や並列回路は回路シミュレータを使用すれば簡単に計算できます。
回路シミュレータと聞くと難しそうに感じるかもしれませんが、一度使い方を覚えてしまえばずっと役立つものなので、余裕があれば使ってみてください。
ちなみに無料の回路シミュレータはいくつか種類がありますが、わたしは「QucsStudio」をおすすめしています。
下記の記事でインストール方法を紹介しているので、ぜひチャレンジしてみてください。
今回は以上です。
最後まで読んでいただき、ありがとうございました。