【図解】コンデンサの原理
コンデンサの原理は、高校の物理の授業の中で交流の電気回路とともに習いますが、その原理や実際の使い方については結局あまり理解できていないという方も多いのではないでしょうか?
そこで今回は、コンデンサの原理を改めておさらいするとともに、実務においてどのような役割を果たすのかを解説します。
動画はコチラ↓
コンデンサとは
教科書によく出てくるのは2枚の金属板が向かい合ったような部品ですね。
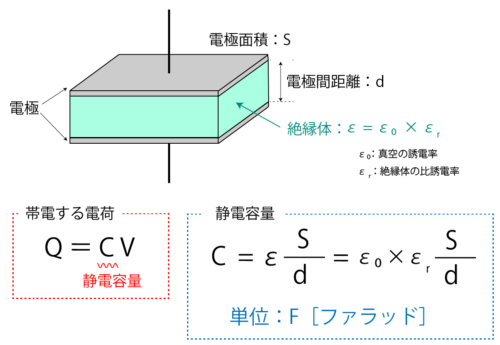
このコンデンサには電気を貯める性質があります。
電極の両端の電圧を V 、電荷の量を Q とすると
Q = CV で電気を貯めた量(帯電する電荷の量)を表すことができます。
静電容量
上の式中の C が静電容量で、回路設計する場合には定数と呼ばれます。
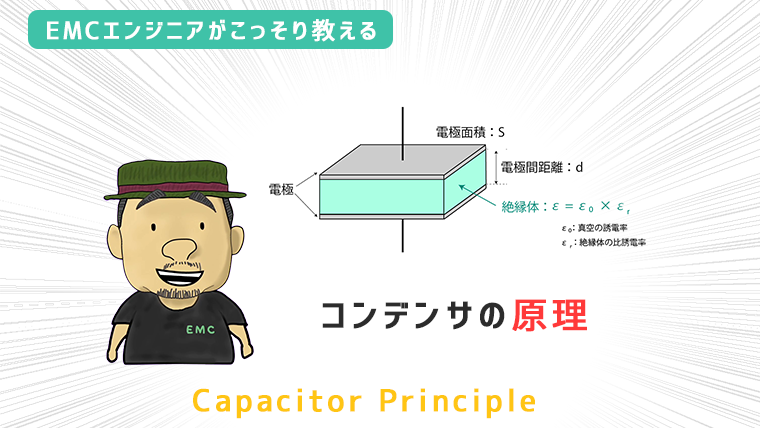
この静電容量は、どれくらい電気を貯められるかを表す係数で、電極の面積を S、電極間の距離を d 、電極間に挟まれた絶縁体の誘電率を ε とすると
静電容量 C = ε* S / d として求めることができます。
- 電極の面積が大きいほど、静電容量が大きくなる
- 電極間の距離が近いほど、静電容量が大きくなる
ただし、静電容量の大きいものほど部品サイズが大きくなる傾向にあります。
誘電体
実際のコンデンサにおいては、小さい部品サイズで大きい静電容量が得られるよう、電極間に誘電率の高い絶縁体を挟んでいます。
代表的な絶縁体としては、ポリエチレンやポリプロピレンといった「プラスチック」、「電解液」を染み込ませた紙、さらには「セラミック」などがあります。
コンデンサの種類の詳細はコチラ↓
単位
静電容量の単位は F[ファラド] で表され、実務的な単位としては「uF」や「pF」といった単位が使われます。
マイクロが 10^-6、ピコが 10^-12 ということで、「uF ~ pF」で表せる範囲の静電容量が実務的によく使用される静電容量になります。

直流回路での役割
直流の電気回路は、オームの法則によって回路の性質を表すことができます。
このオームの法則に基づいてコンデンサの性質を考えてみると、コンデンサは2つの電極が絶縁体を介して配置されているということで、当然2つの電極間には電気的なつながりはありません。
そのため抵抗という観点で考えると、抵抗値は R = ∞Ω になります。
電荷の振る舞い
この時の状態を電子レベルで考えてみます。
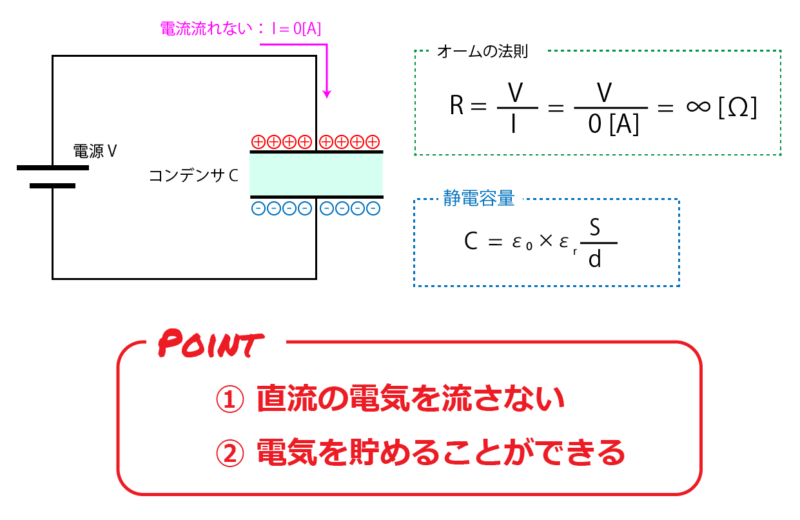
ある電源がコンデンサに接続されていたとすると、コンデンサの電極には、電圧に応じてプラスの電荷とマイナスの電荷が帯電します。
この電極に帯電した電荷は、プラスとマイナスが釣り合った状態でそのエネルギーを保持します。
これがコンデンサが電気を貯めることができると言われる所以で、誘電率の高い絶縁体を電極間に挟むことで、より多くの電荷を蓄えることができます。
このようにコンデンサは、直流回路において
- 直流の電気を流さないこと
- 電気を貯めること
この 2つが最も重要な役割となります。
直流での用途
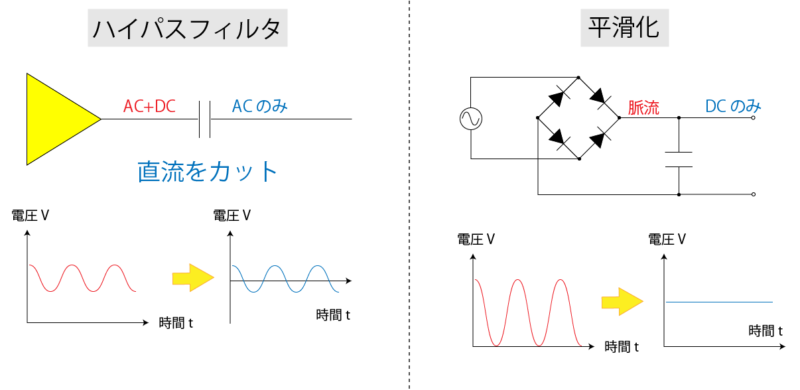
この2つの性質は、実務ではハイパスフィルタや平滑回路として使われています。

交流回路での役割
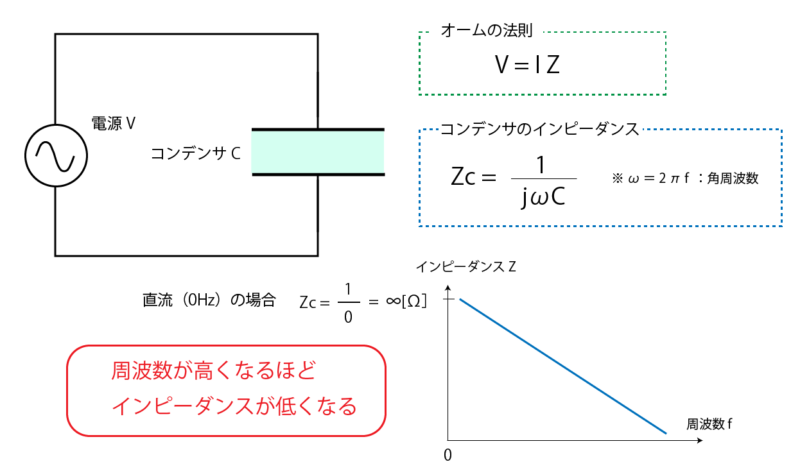
交流回路を考える場合も基本はオームの法則です。
交流回路の場合は、抵抗 R の部分がインピーダンス Z に変わります。
インピーダンスの詳細はコチラ↓

インピーダンスは交流の電気の流れにくさを表すもので、ベクトルとして表されます。
コンデンサは、交流の周波数が低い場合には電流がほとんど流れず、反対に周波数が高くなるほど電流が流れやすくなるという特徴を持ちます。
直流は周波数が「0 Hz」で、 f = 0 をインピーダンスの式に代入すると Zc = ∞Ω となることから、先ほどの直流回路での説明と矛盾はありませんね。
電荷の振る舞い
交流回路におけるコンデンサの性質を電子レベルで考えてみます。
ここでは正弦波の位相 0°の位置からスタートして、位相が進むことでどのように電荷の状況が変わっていくかを見ていきます。
まず位相が 0°の位置においては、コンデンサには電圧が掛かっていないため、それぞれの電極は平衡状態となっています。
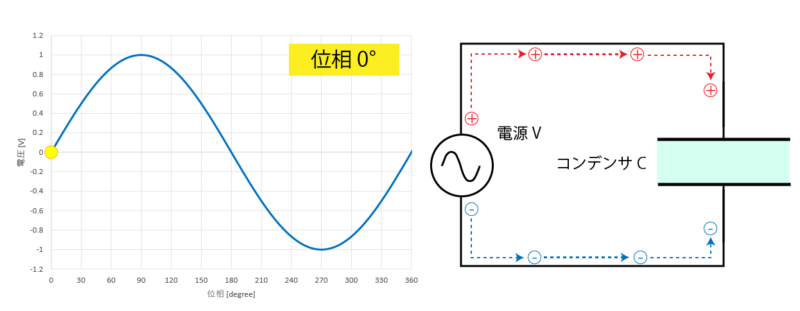
ここから徐々に位相が進んでいくと、コンデンサの両端にはプラスとマイナスの電荷が徐々に帯電していき
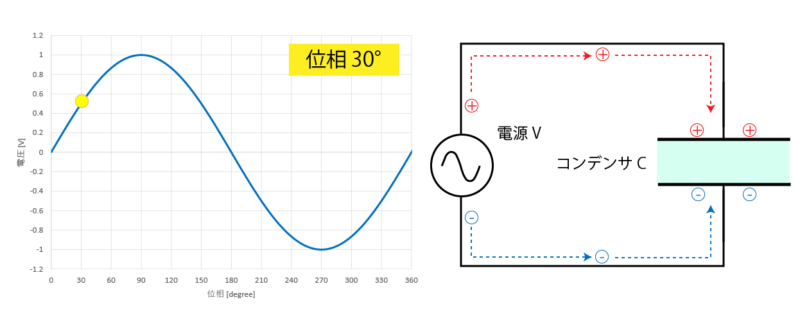
位相が 90°の位置に来たとき、正方向の最大の電圧がコンデンサの両端に掛かります。
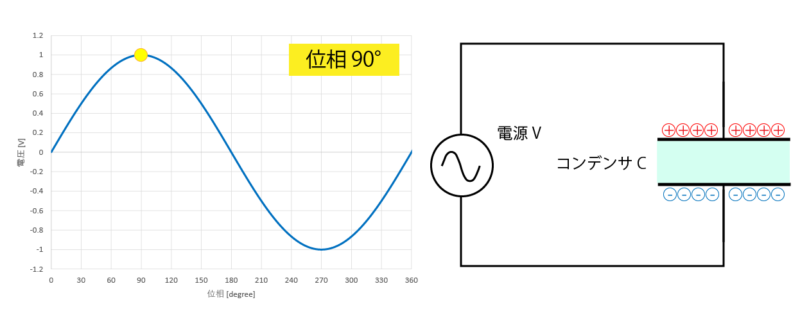
このときコンデンサは、最も電荷が蓄えられた状態となります。
そして 90°から位相を進めていくと、正方向の電圧が徐々に低下していきます。
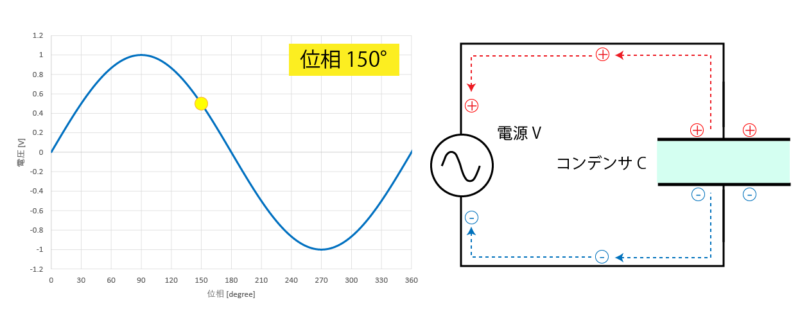
位相が 180°に達すると、両端の電荷は 0 となり平衡状態に戻ります。
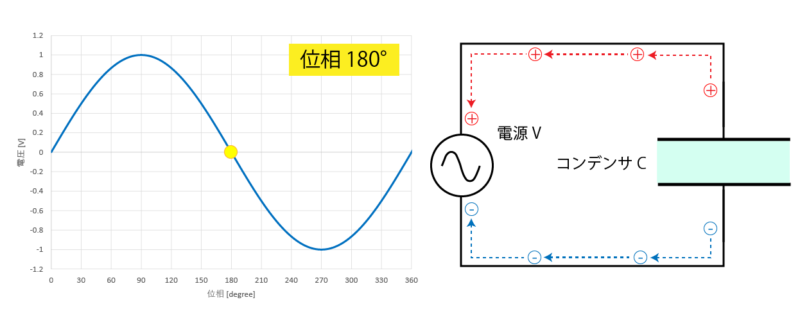
そこから更に位相を進めると、プラスとマイナスの電荷が逆向きに帯電していきます。
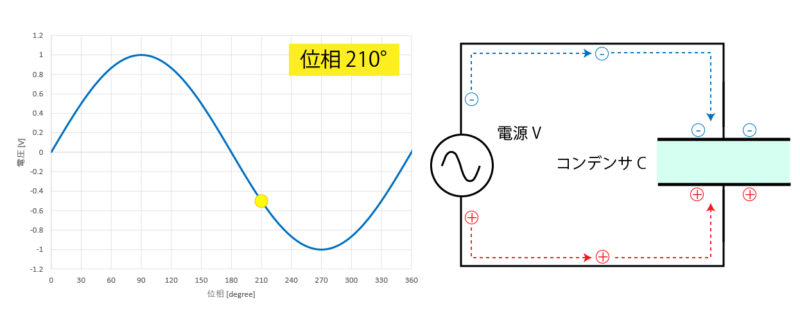
位相が 270°に達すると、再び最も電荷が蓄えられた状態となります。
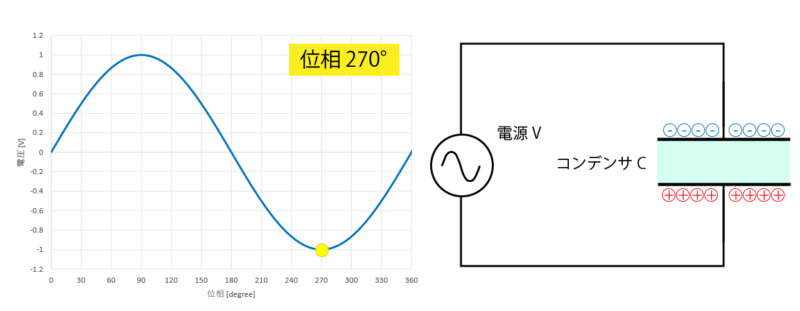
そして位相が270°を超えると、電極に帯電する電荷が減っていき
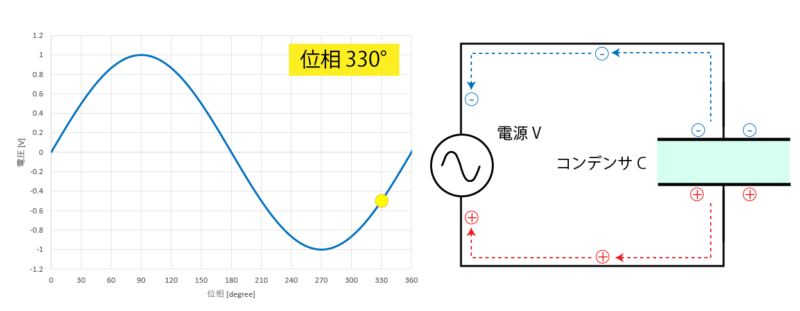
最終的に位相が 360°となると、もとの平衡状態へ戻ります。

電圧と電流の関係
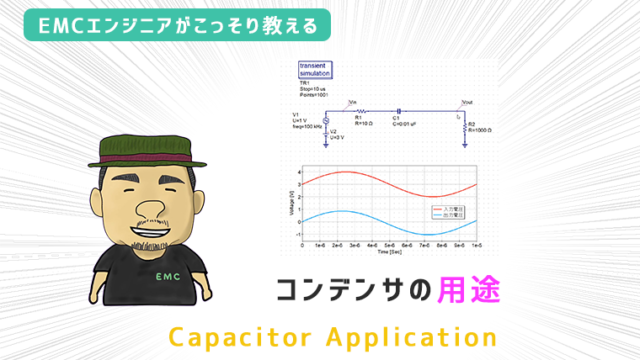
このときにコンデンサに掛かる電圧と電流の関係を見てみます。
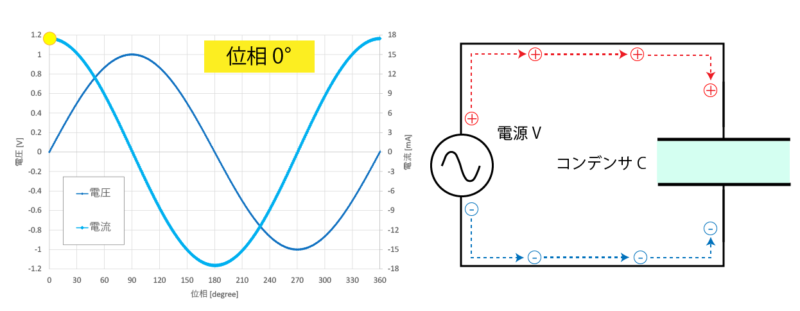
電圧の波形と電流の波形を比較すると、電流が電圧よりも位相が 90°前倒しになった波形となっており、このことからコンデンサは「位相を進める」性質を持つと言われます。

周波数とインピーダンスの関係
コンデンサのインピーダンスは、周波数が高くなるほどインピーダンスが低くなるとお伝えしましたが、この理由についても考えてみましょう。
電圧と電流は位相が90°異なりましたが、これを別の言い方にすると、電流は電圧を微分したものと捉えることができます。
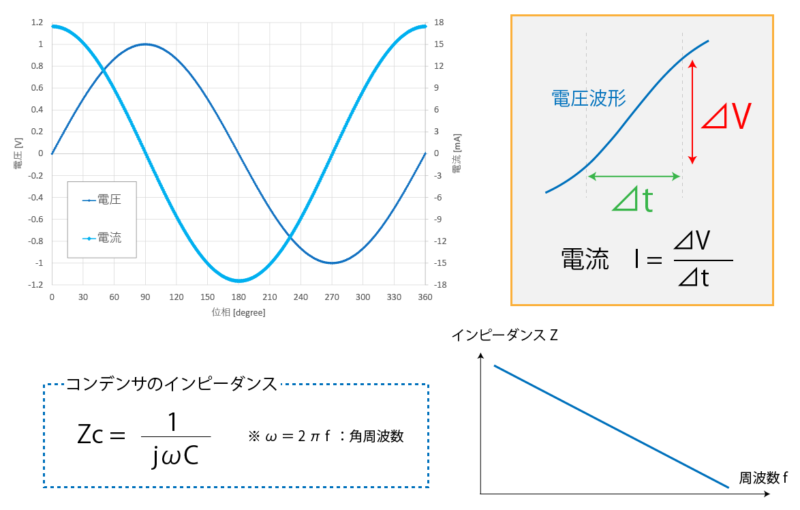
微分と聞くと難しく聞こえるかもしれませんが、つまりは「電流の大きさ」は「電圧の傾き」によって決まるということです。
電圧は「電位差」と呼ばれるように、電気回路における位置エネルギーを表したものです。
そして位置エネルギーは、2点間の距離が大きいほど高いエネルギーを持つということで、電気回路においても2点間の電位差が大きいほど大きな電流が流れます。
そして、電圧波形をある時間単位に区切って見ると、位相が 0°あるは 180°となったときに2点間の電位差、つまりは傾きが最も大きくなることから、回路に流れる電流もこのときに最大となります。

ではここで周波数が高くなるとどうなるでしょうか?
周波数が高くなるということは 1秒間に振動する回数が多くなるということで、これを傾きとして捉えると、周波数が高くなるほど傾きが大きくなります。
これはすなわち、周波数が高くなるほど電流が大きくなるということで、これが周波数が高くなるほどコンデンサのインピーダンスが低くなる理由となります。
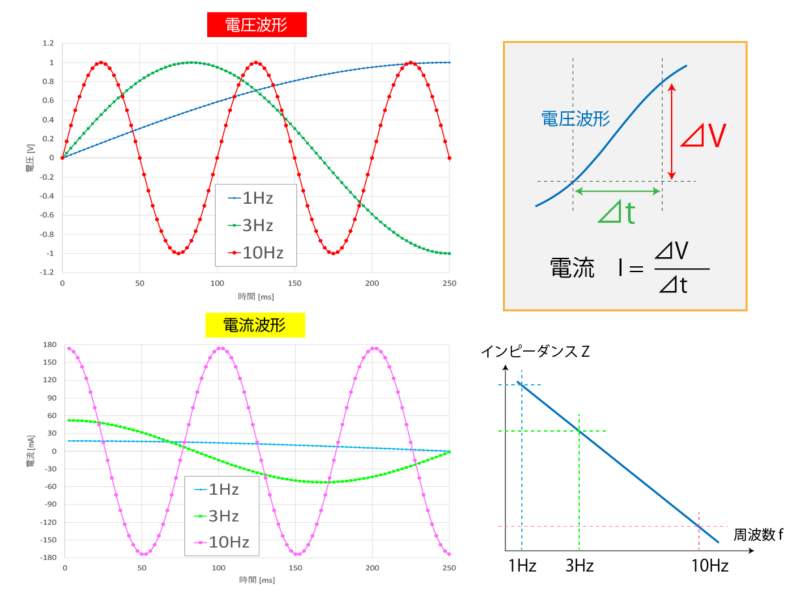 周波数ごと電流値の比較
周波数ごと電流値の比較さらに回路の流れる電流の最大値は静電容量によって決まりますが、静電容量は絶縁体の誘電率に比例して高くなることから、誘電率が高いものほどインピーダンスが低くなります。
交流での用途
交流回路においてコンデンサは
- 電流の位相が進むこと
- 周波数が高くなるほどインピーダンスが低くなること
この 2つが最も重要な性質となります。
この2つの性質は、実務では様々な場面で出てきますが、代表的な例としては力率補正回路やフィルタ回路があります。
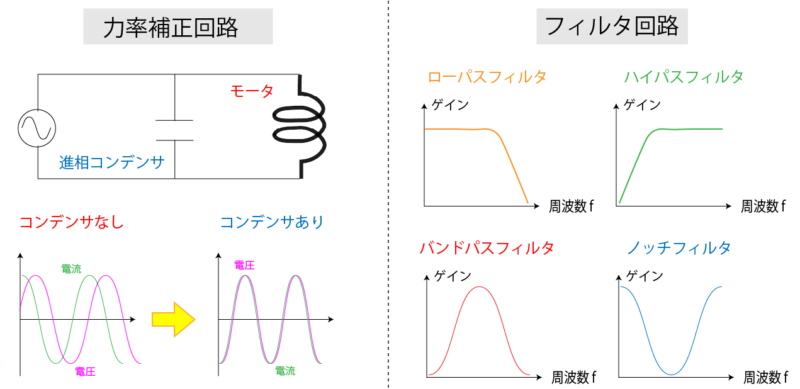
このうち力率を補正するためのコンデンサは「進相コンデンサ」と呼ばれ、誘導性の負荷による力率の悪さを改善する働きを持ちます。
フィルタ回路に関しては、コンデンサを直列に接続した場合にはハイパスフィルタとして働くことはもちろん、回路に対して並列に接続することでローパスフィルタとして機能させることも可能です。
またハイパスとローパスの両者を組み合わせたバンドパスフィルタ や ノッチフィルタ もあり、いずれ用途も周波数が高くなるほどインピーダンスが低くなるというコンデンサの性質を利用したものになります。
フィルタの詳細はコチラ↓

おわりに
今回はコンデンサの原理として、直流回路と交流回路それぞれの場合のコンデンサの働きについて解説しました。
直流と交流、それぞれの回路でのコンデンサの性質は、電気回路を理解する上で非常に重要となる知識です。
そのため、原理まで含めてきちんと理解しておくようにしてくださいね。
実際にコンデンサを使う時の選び方はコチラを参照ください↓

今回は以上です。
最後まで読んでいただき、ありがとうございました。