信号の種類と周波数特性

ノイズ対策において、信号波形がどのような周波数成分を持っているかを把握しておくことは非常に大切です。

そこでこの記事では、電解回路や高周波回路でよく見かける波形の周波数特性を紹介します。

 

直流

理想的な直流は、時間軸上で振幅が変化しない波形になります。

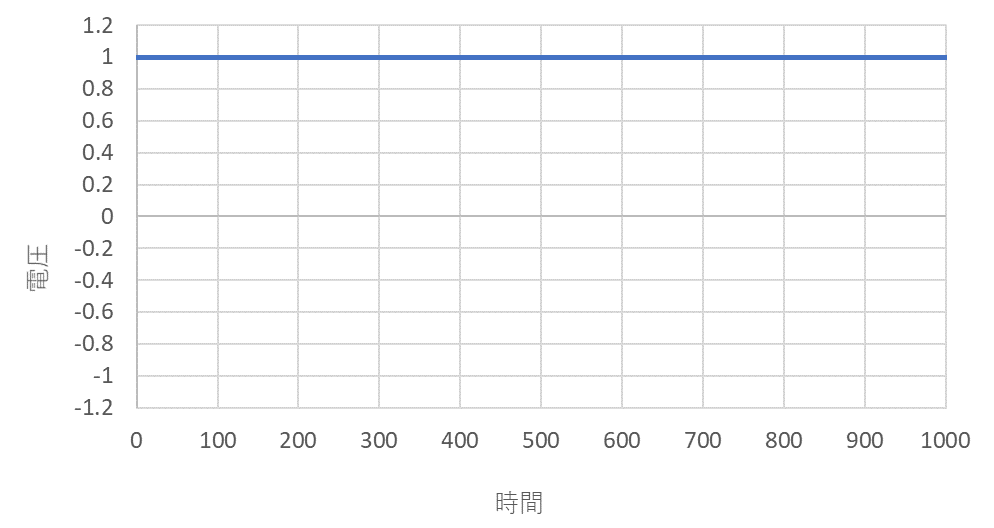
周波数特性としては、振幅が時間的に変化しないため 0Hz ということになり、ノイズ問題を引き起こすことはほとんどありません。

 

 

正弦波

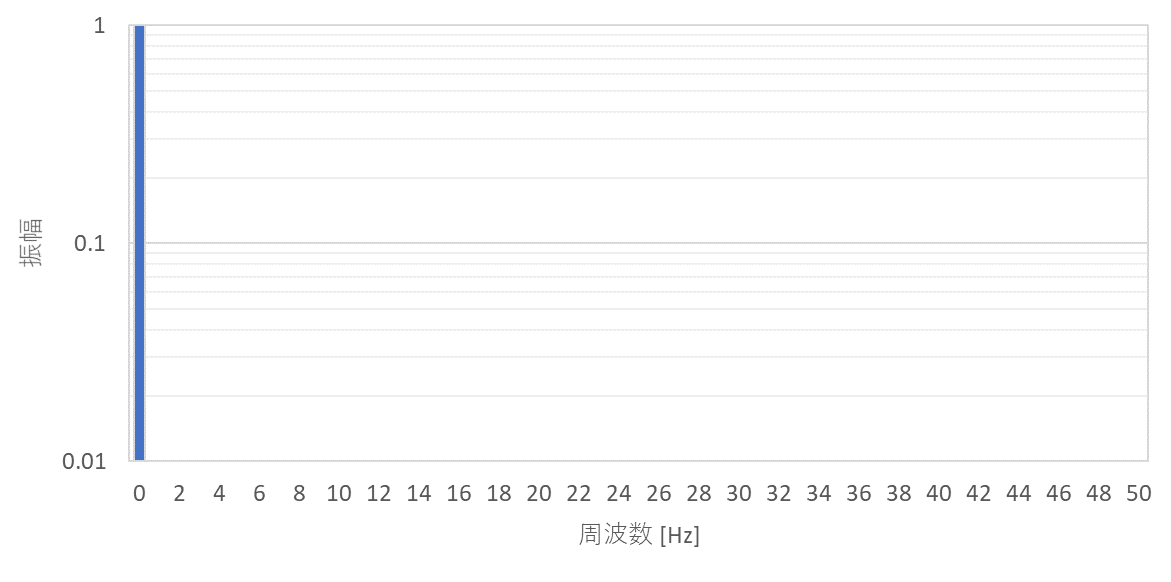
正弦波は一定の周期で振動する波形です。

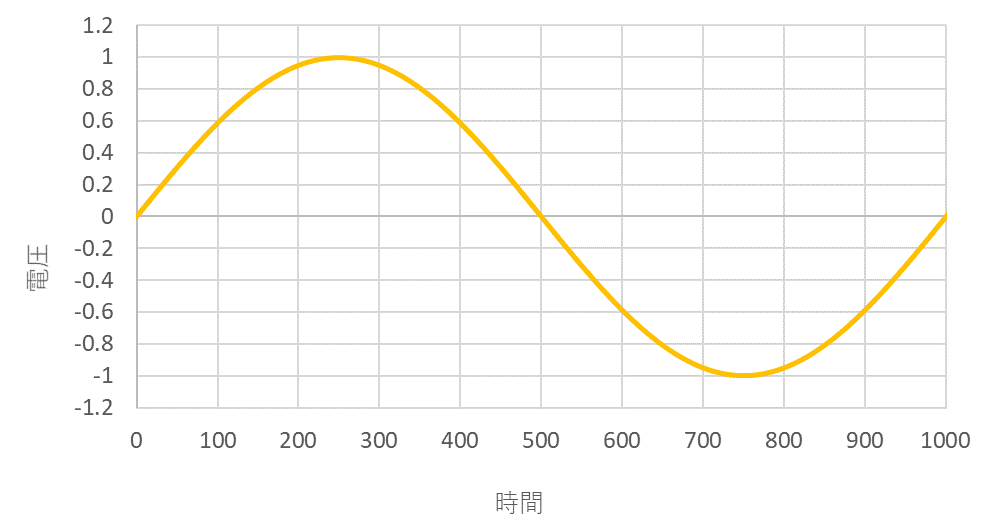
周波数特性は、単一の周波数でのみ振幅を持つスペクトルになるため、ノイズ問題を引き起こすことはほとんどありません。

 

矩形波

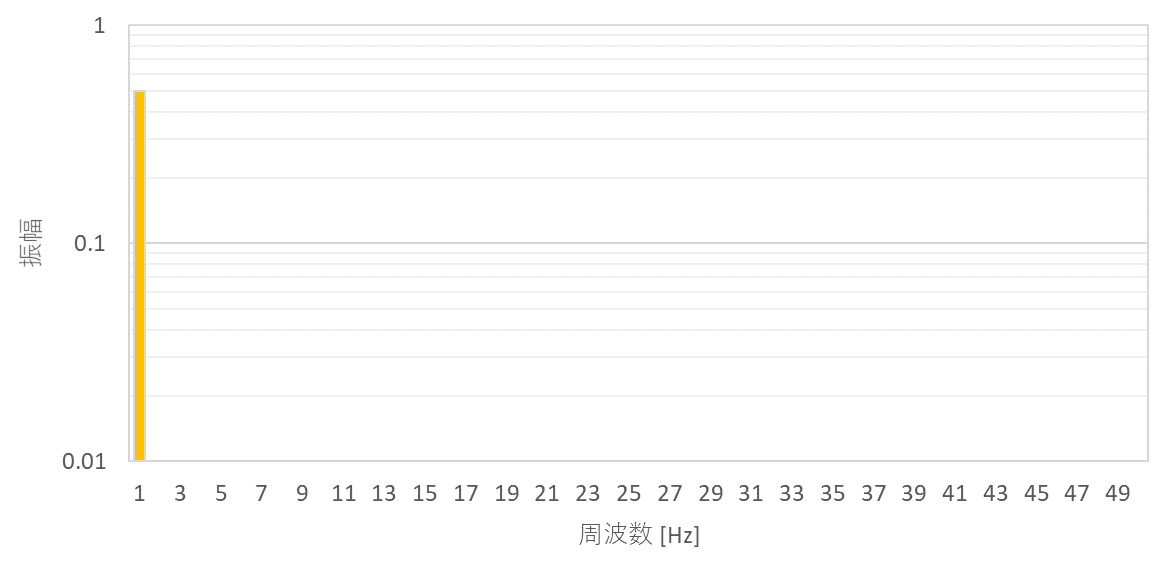
矩形波は、デジタル回路の信号伝搬に使用される波形で、0と1の2つの値しか持ちません。

そして、０から１、あるいは１から０に変化する時間（遷移時間）が非常に短いことが特徴として挙げられます。

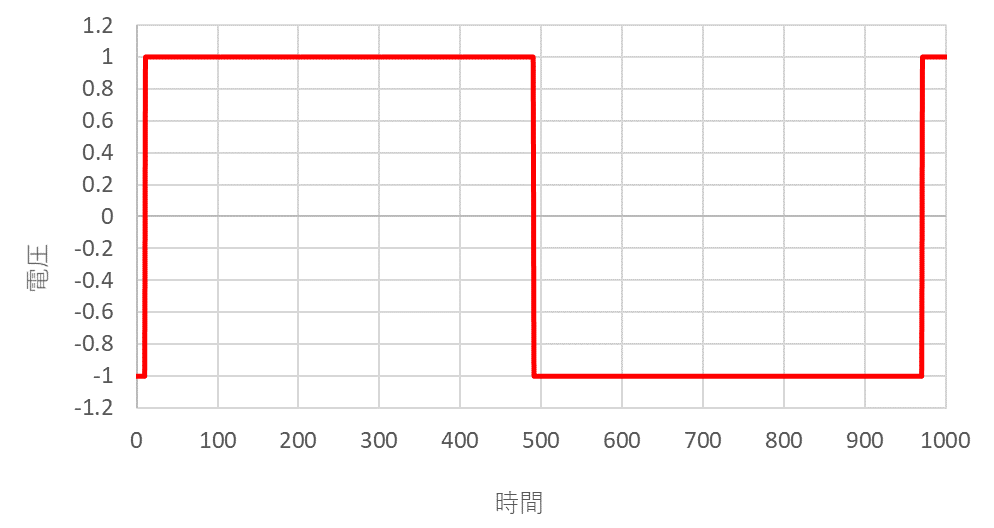
このような矩形波は、繰り返し周波数に相当する基本波と、その整数倍の高調波成分を持ちます。

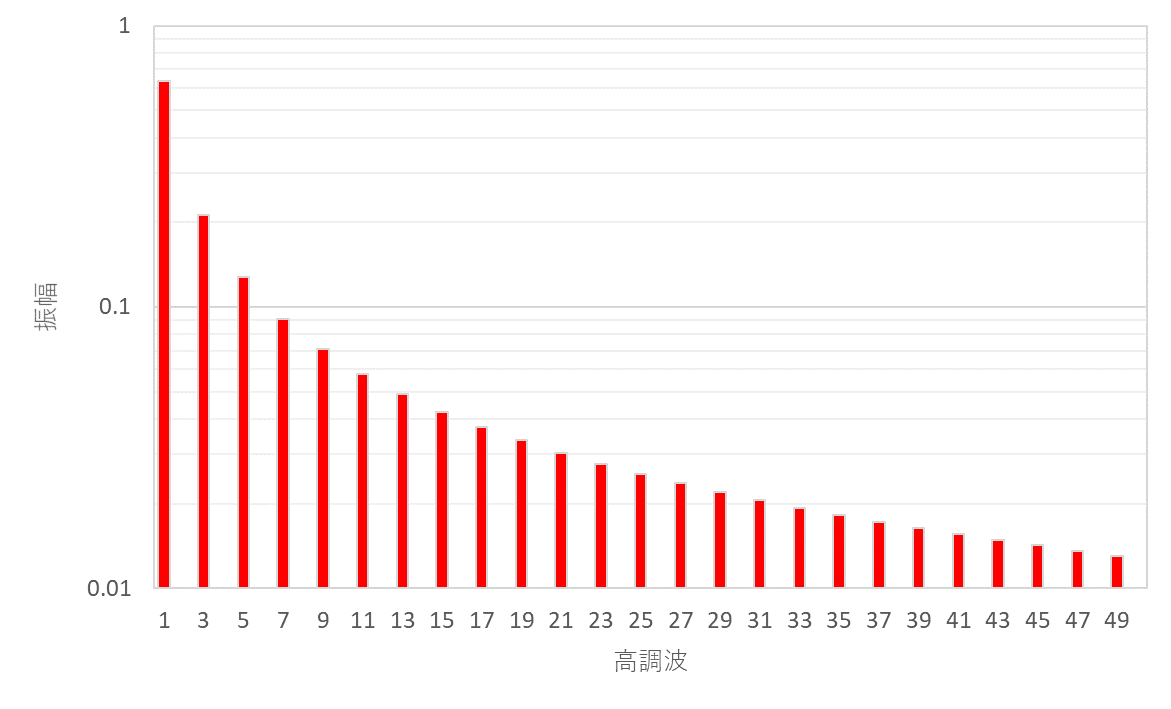
矩形波の周波数特性については、下図のように高調波を一つずつ足し合わせていくと、徐々に矩形波に近づいていくことからイメージできます。

【基本波～５倍高調波】

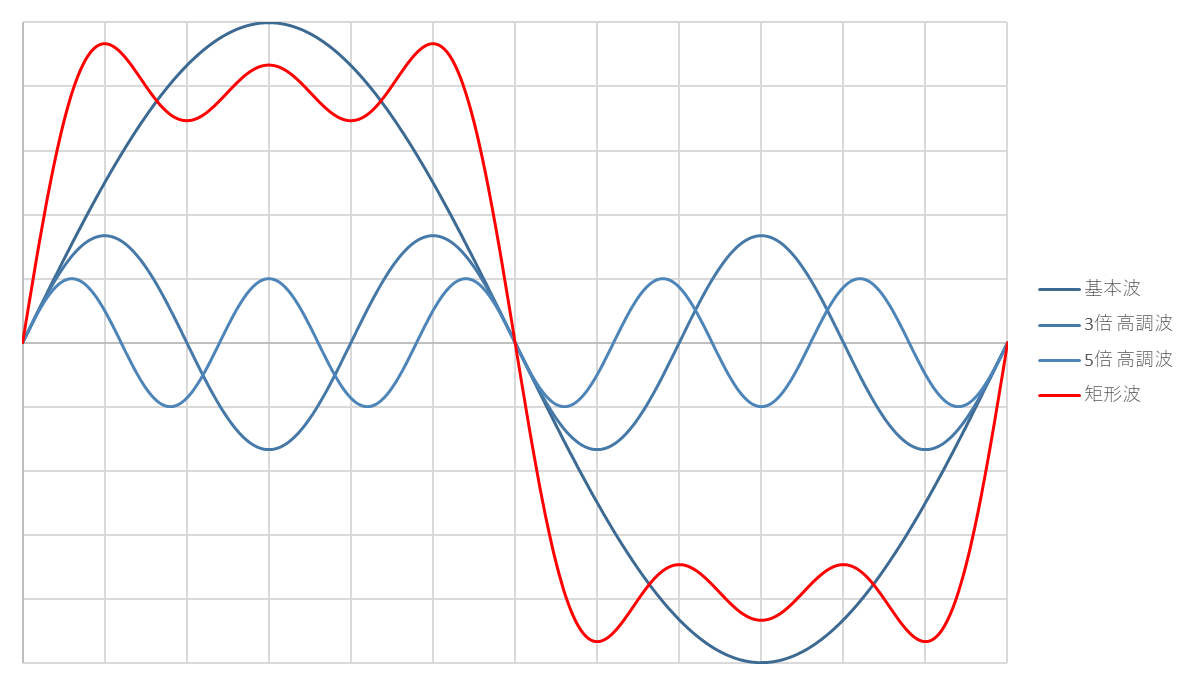
【基本波～15倍高調波】

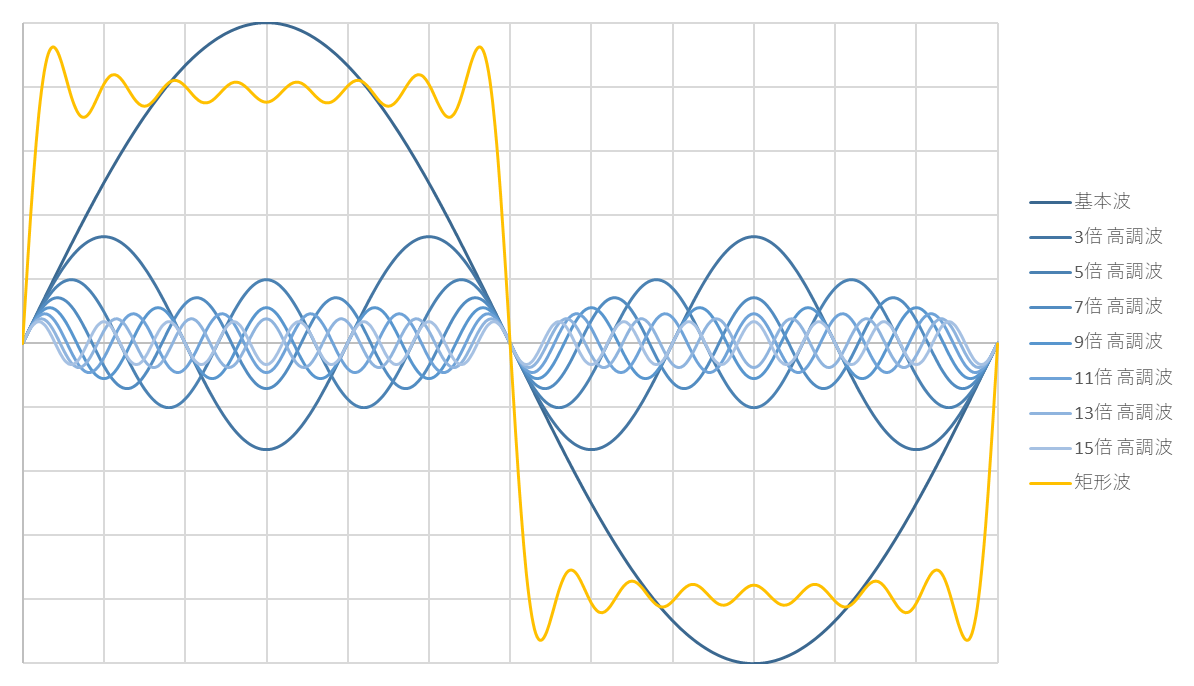
【基本波～25倍高調波】

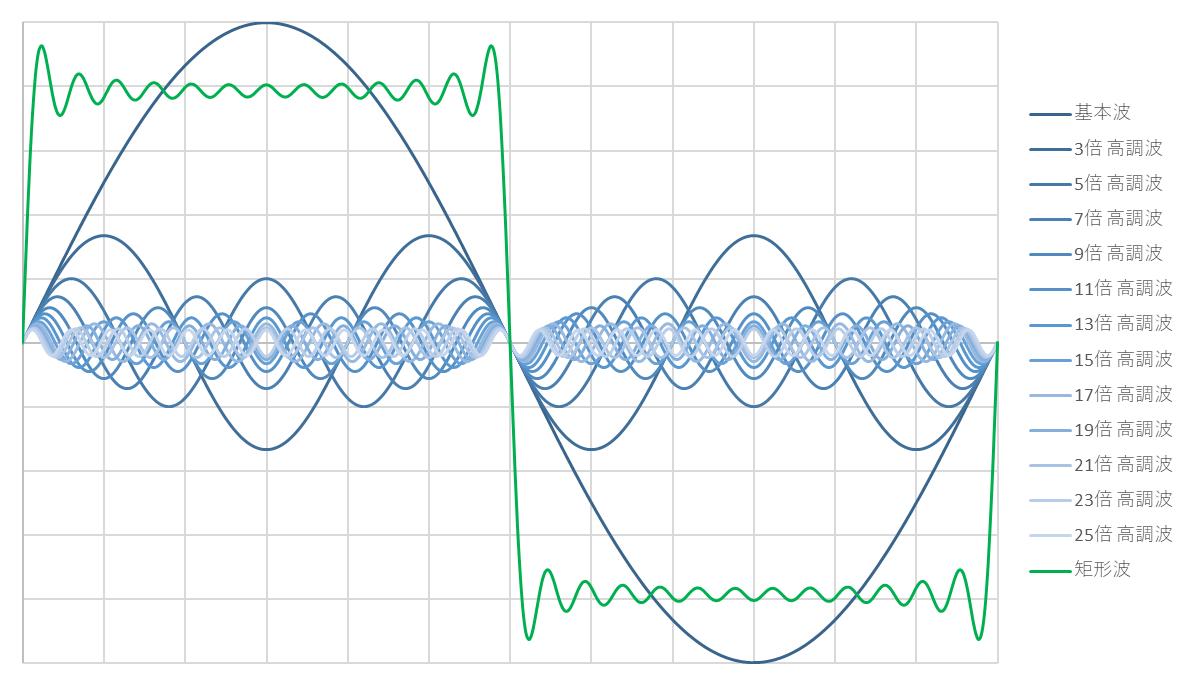
矩形波のスペクトラムは、以下のような特徴を持ちます。

 

 

のこぎり波

のこぎり波は、PWM変調のキャリア信号として使用されています。

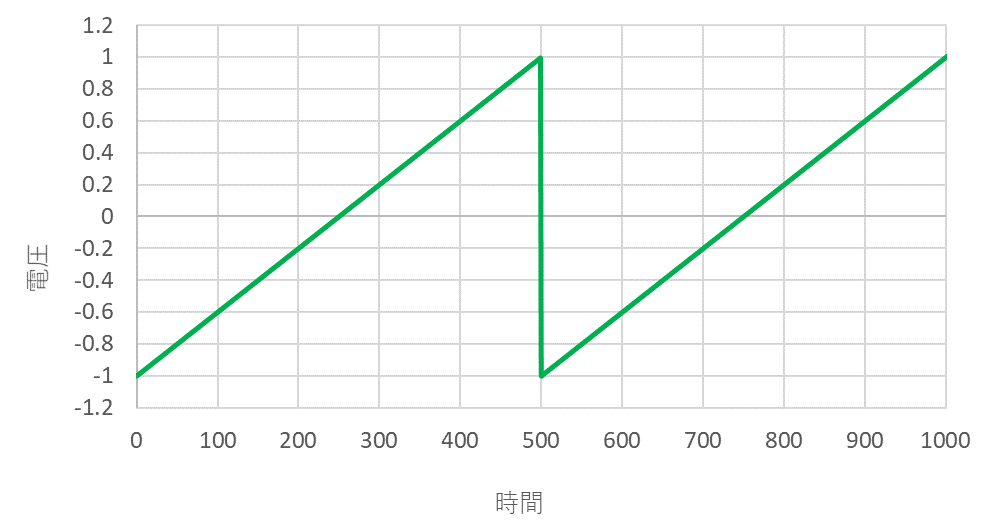
のこぎり波の周波数特性は矩形波と同様に、広い周波数帯で振幅が上昇します。

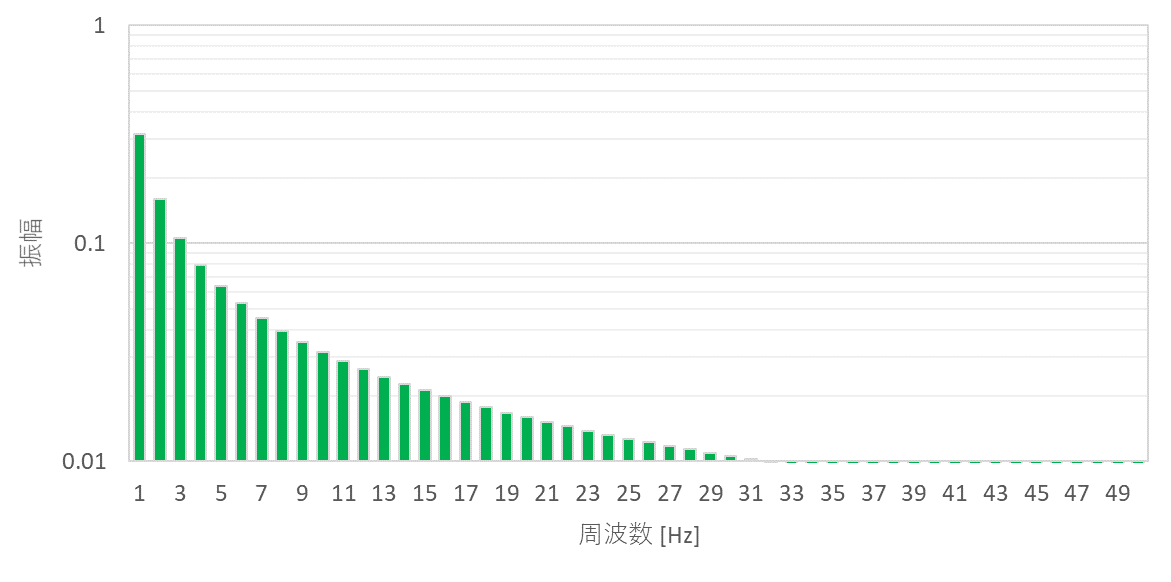
信号の帯域幅は、信号の立ち上がり／立ち下がり時間（遷移時間）によって決まり、以下の式からおおよそ見積もることができます。

 

インパルス波形

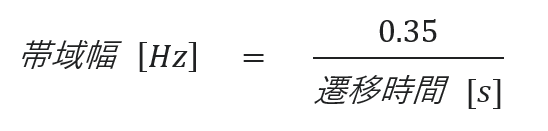
遷移時間が短い波形としてはパルス波形があり、このパルス波形の中でも非周期的に発生するもののことをインパルス波形と呼びます。

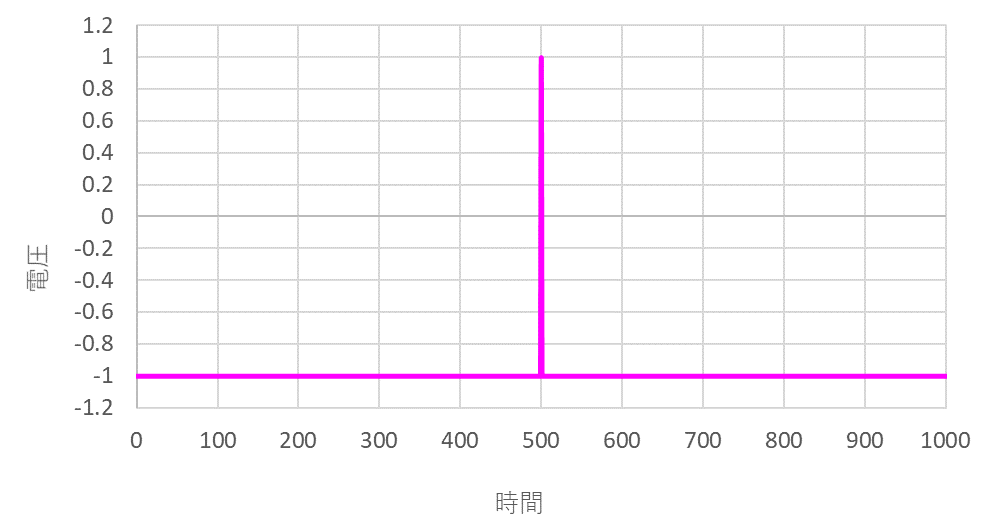 このインパルス波形も過渡時間に応じて、広い周波数帯で振幅が上昇します。

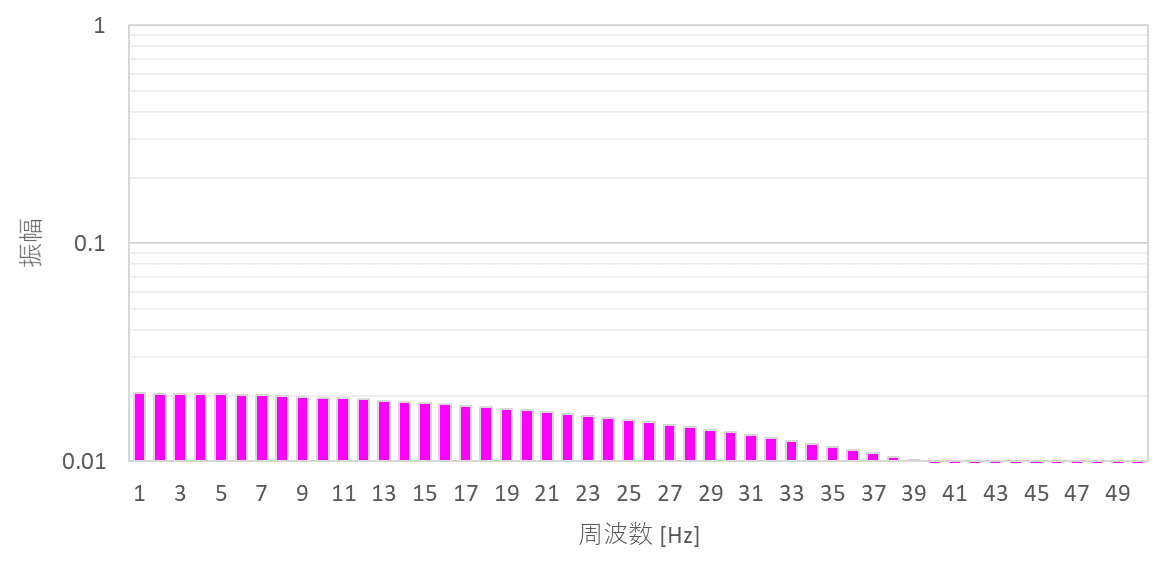
ノイズ問題として考える場合には、様々な周波数成分を含んでいるため、非常にノイズ問題を引き起こしやすい波形となります。

 

 

AM変調波

AM変調（Amplitude Modulation）はアナログ変調方式の１つで、イミュニティ試験でも使用される波形になります。

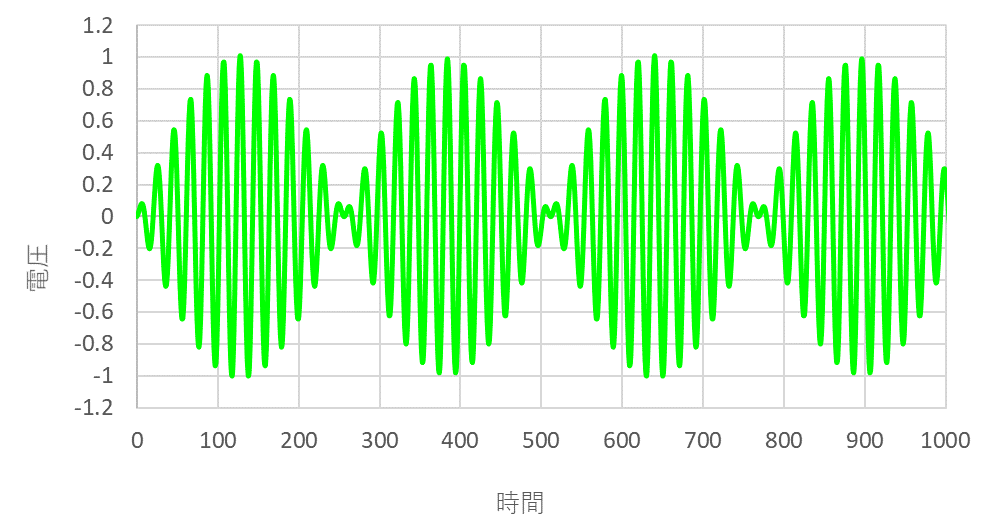
AM変調波の周波数特性は、キャリア信号の周波数を基準として、アナログ信号の周波数帯に応じてスペクトルが広がっていきます。

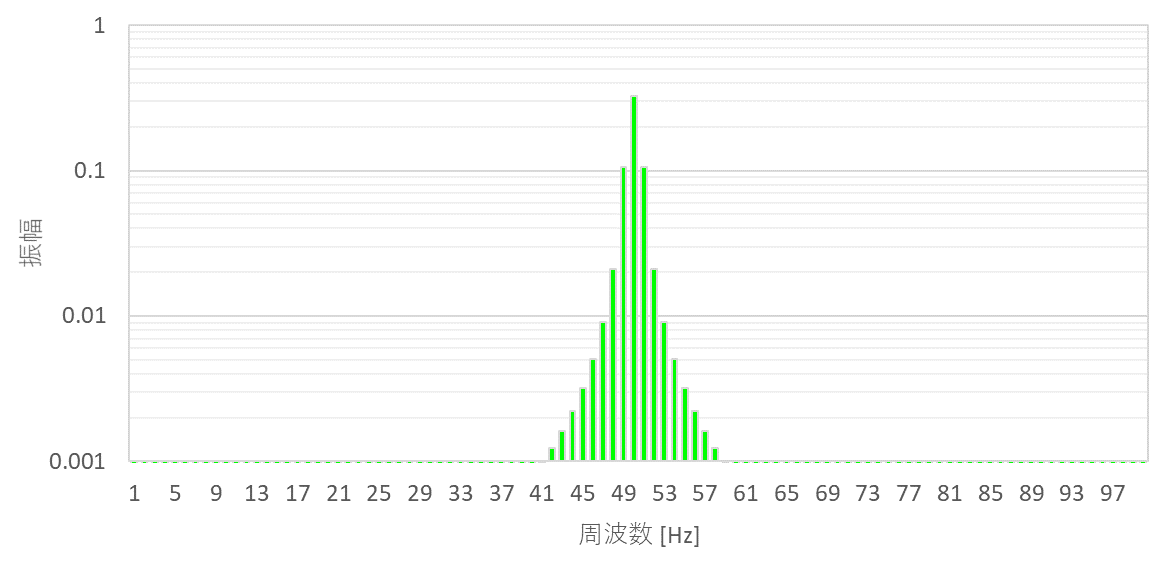
ラジオの受信機の場合、このAM変調波の帯域に別の信号の周波数成分が含まれていると、受信障害としてノイズの影響を受けます。

 

おわりに

今回は、電気回路や高周波回路で出てくる代表的な波形の周波数特性を紹介しました。

時間軸と周波数軸でそれぞれの波形の特徴を理解できれば、ノイズ対策においても効率よく発生源を見つけることができます。

波形の周波数特性に関しては、オシロスコープのFFT機能を使用すれば簡単に確認する事ができるので、デバッグの際には確認しておくことをおすすめします。

 

今回は以上です。

最後まで読んでいただき、ありがとうございました。