【入門】キルヒホッフの法則とは?
オームの法則と並んで、電気回路において重要な法則が「キルヒホッフの法則」です。そこでこの記事では、キルヒホッフの法則の原理について解説します。
動画はこちら↓
キルヒホッフの法則の概要
電気回路で最も基本となる法則は「オームの法則」です。
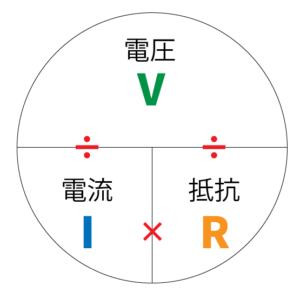
このオームの法則は、単純な電気回路の振る舞いを理解するためには非常に重要です。
一方で少し複雑な回路、例えば電圧源が複数存在したり、1つのノード(節点)に複数の入出力が存在したりする場合には、オームの法則だけでは回路の振る舞いを理解するのが難しくなります。
そんな回路に対して、有効になる考え方が「キルヒホッフの法則」です。
このキルヒホッフの法則は、2つの法則から成り立っています。
- キルヒホッフの第一法則(電流則)
- キルヒホッフの第二法則(電圧則)
この2つの法則は、いずれも複雑な回路の特定のポイントに着目することで回路を簡略化するためのものです。
用語だけ見ると難しそうに感じますが、概念そのものは比較的簡単なので電気回路を学ぶ上では必ず理解しておく必要があります。
学校の教科書などでは計算問題として出てくるため苦手意識を持つ方も多いかもしれませんが、実務においては概念さえ理解できていれば問題ありません。

キルヒホッフの第一法則(電流則)
キルヒホッフの第一法則は「電流則」とも呼ばれており、回路中の電流に着目した法則になります。
回路上のあるノード(節点)に流れ込む電流の総和と、そこから流れ出る電流の総和は等しい
文章にすると少し難しそうに感じますが、要するに「全てのノードで電流の入出力の総和が 0になる」ということです。
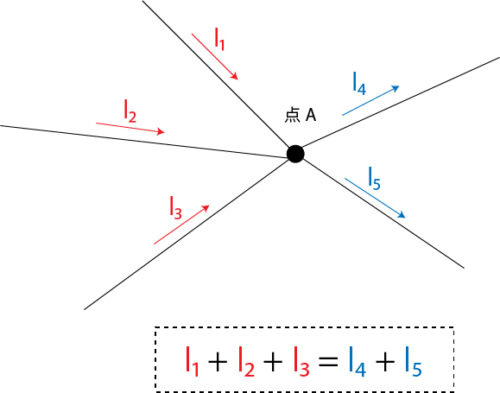
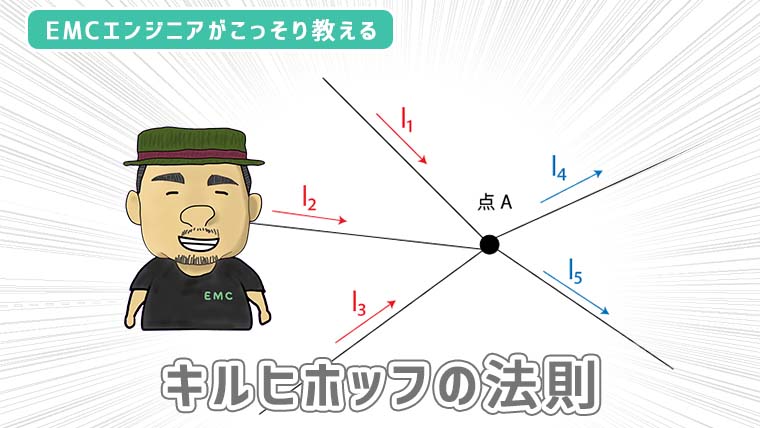
この考え方を電気回路の落とし込んだものが下図です。
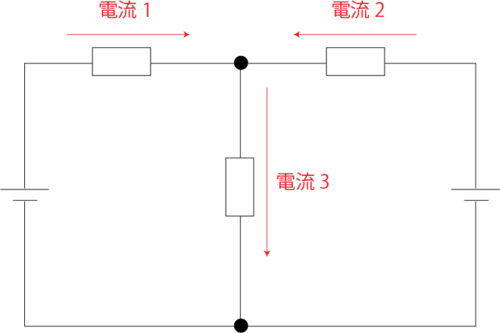
この回路において、点Aには「電流1」と「電流2」が入力されて「電流3」として出力されています。
これに電流則を適用すると「電流3=電流1+電流2」という関係性が成り立ちます。電流則というと難しそうに聞こえますが、言わんとすることはたったこれだけです。
では、なぜこの電流則が重要なのかと言うと、このように回路の一部を取り出すことで、回路全体の振る舞いを計算するのが簡単になるためです。
例えば上の例においては、回路の点Aを境界として、右側の回路と左側の回路に分けて連立方程式を解くことで回路全体の振る舞いを求められます。
とはいえ、実務においてこのような計算はシミュレータに任せてしまえばいいので、とりあえずは電流則の概念だけ理解しておけば問題ありません。

キルヒホッフの第二法則(電圧則)
キルヒホッフの第二法則は、「電圧則」とも呼ばれており、回路中の電圧に着目した法則になります。
ある閉回路の電源電圧(起電力)の総和と、負荷で消費される電圧(電圧降下)の総和は等しい
ここでまず理解しておくべきは「電圧降下」についてです。
電圧降下とは、ある負荷によって消費されるエネルギーを電圧によって表したもので、オームの法則をもとに計算することができます。

そして電圧則においては「閉回路において電圧降下の総和が回路の電源電圧と必ず等しくなる」という関係性に着目します。
この電圧則も文章にすると難しく感じますが、オームの法則を理解できていれば考え方はすぐに理解できはずです。
そしてこの考え方は、電圧源が複数存在したり、負荷が直並列に入り組んで配列されている場合において普遍的に機能するものなので、回路の振る舞いを理解する上で重要になります。

キルヒホッフの法則の解析例
資格試験の学習をしているのであれば、計算式を解く必要がありますが、実務においては回路シミュレータを使用して計算すれば良いので、自分の計算能力はそこまで重要ではありません。
ここでは、キルヒホッフの法則に関連した問題について、回路シミュレータ(QucsStudio)を使って解析し、その中で「電圧則」と「電流則」がどのように機能しているかを解説します。
解析例1
1つ目の解析例は、キルヒホッフの法則を利用した問題としてよく出題される2つの電源が接続された回路です。
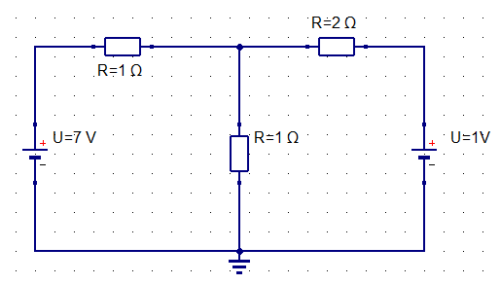
この回路には、左右のそれぞれの閉回路に電源が接続されており、電流則に基づきそれぞれの回路によって足し合わされた電流が中央の「1Ω」の抵抗に流れます。
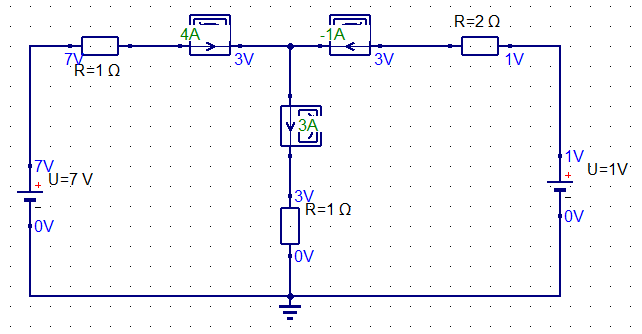
上図においては、左側の閉回路の電流が「4A」、右側の閉回路の電流が「-1A」となっており、この電流の総和である「3A」の電流が 1Ωの抵抗に流れています。
また電圧則についても、回路を少し変形すると理解しやすいです。
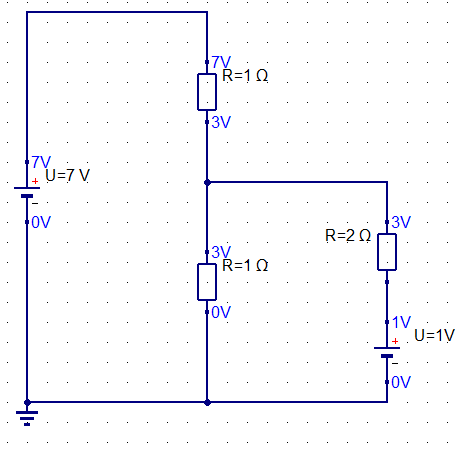
電圧源「7V」に対して、抵抗による「電圧降下」が等しくなっていることがわかります。
解析例2
2つ目の解析例は、キルヒホッフの法則に関連したホイートストンブリッジ回路です。

このホイートストンブリッジ回路は、ブリッジ回路が平衡状態のときに中央の抵抗に電流が流れないという性質があり、未知の抵抗を測定するときに用いられます。
この回路では、3つの閉回路に分けて連立方程式を解くとそれぞれの抵抗に流れる電流が求まりますが、ここでも重要なことは電流則に基づくということです。
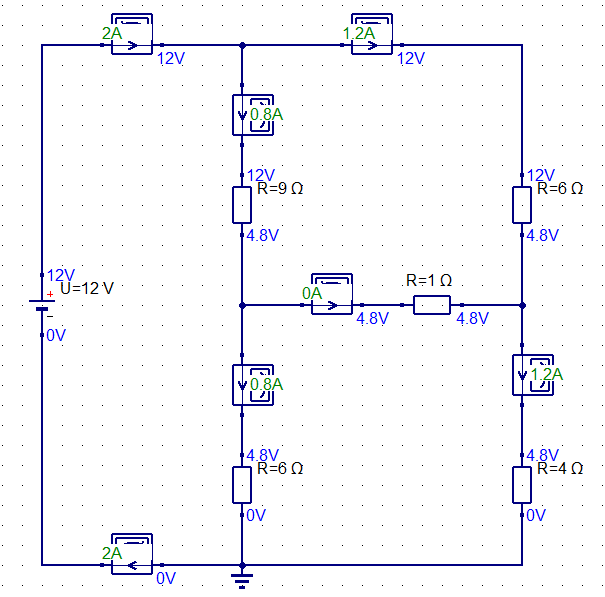
回路全体に流れる電流「2A」に対して、上部のノードで「1.2A」と「0.8A」に分岐しており、また中央の「1Ω」の抵抗に対しては電位差がないため、そのまま下側の回路に同じ電流が流れています。
おわりに
今回はキルヒホッフの法則の概念と解析例について解説しました。
キルヒホッフの法則の「電流則」と「電圧則」は、電気回路のキホンとも呼べる重要な法則で、すべての電気回路に適用可能な概念です。
特に電気は目に見えないものなので、突飛な考え方に惑わされることもあるかもしれませんが、何事も基本的な原理の積み重ねによって事象が生じています。
そのため、基本に立ち返る土台としてこの「キルヒホッフの法則」の「電流則」と「電圧則」を理解しておいてください。
今回は以上です。
最後まで読んでいただき、ありがとうございました。