【図解】インピーダンス入門

インピーダンスは、電子部品の重要な特性の1つとして様々な場面で登場します。そこで今回は「インピーダンスとは何か」について解説します。
動画はコチラ↓
インピーダンスとは

インピーダンス Z は交流における電流の流れにくさを表すもので、単位は Ω [オーム] で表されます。直流回路では電流の流れにくさを「抵抗」で表しますが、インピーダンスはその交流バージョンといった理解でも問題ありません。
もちろんオームの法則にも当てはまりますので、「V=IR」の式を「V=IZ」として表すことができます。
直流と交流の違い
交流回路と直流回路の違いとしては、時間軸で見たときにその大きさが変化することが挙げられます。正弦波で考えるとわかるように、時間が進むにつれて大きさが変わっています。そのため交流回路では、振幅と位相によってこの波の性質を表します。
そして交流回路は位相を持つことによって、単純な大きさではなく向きを持った量、つまり「ベクトル」として表されます。
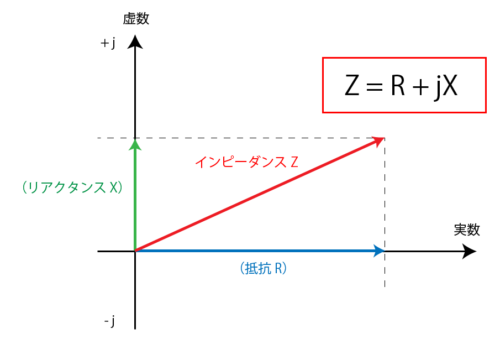
インピーダンスの場合は、横軸が「抵抗 R」、縦軸が「リアクタンス X」として表され、抵抗が損失の大きさ、リアクタンスが位相の変化量に相当します。

インピーダンスの詳細
「Z=R+jX」という式において、リアクタンス X は「誘導性のリアクタンス」と「容量性のリアクタンス」の2つの種類に分かれます。
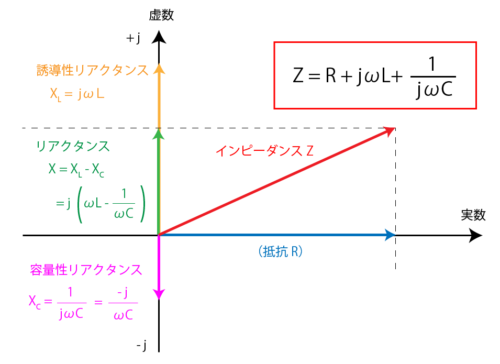
この誘導性と容量性は、それぞれコイルとコンデンサを意味しており「Z=R+jωL+1/jωC」に変形することができます。( ω は角周波数で ω=2πf )
リアクタンスのXの部分が「jωL」 と「 1/jωC 」に変わっています。
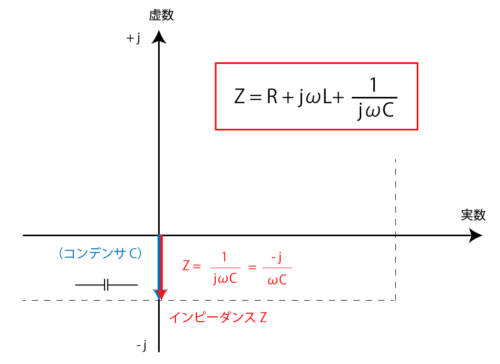
このうち誘導性のリアクタンスは、その大きさを jωL として縦軸のプラス方向にプロットします。一方、容量性リアクタンスは、1/jωC のままでは 虚数 j が分母にありグラフにプロットできないため -j/ωC と変形し、縦軸の負の方向にプロットします。
そして誘導性リアクタンスと容量性リアクタンスは、それぞれ180°向きが異なるため、それぞれの差分が全体としてのリアクタンスの大きさ X ということになり、更にはそのリアクタンス X と抵抗 R の交点を指すベクトルがインピーダンス Z ということになります。

インピーダンス特性
「抵抗」「コイル」「コンデンサ」のそれぞれの周波数特性を確認します。
抵抗
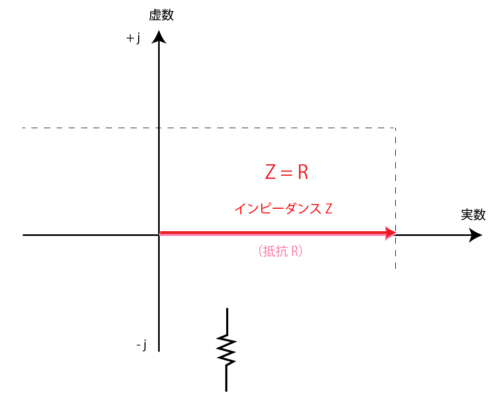
抵抗は、Z=R+jωL+1/jωC で考えると R に相当しますが、Rには何も係数がかかっていないため、交流の周波数が変化しても抵抗のインピーダンスは常に一定の値を示します。
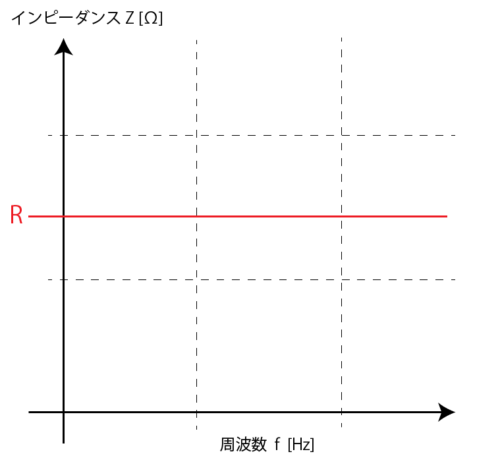
縦軸をインピーダンス、横軸を周波数としてグラフを表すと、真横にまっすぐの直線が引かれた特性となります。
コイル
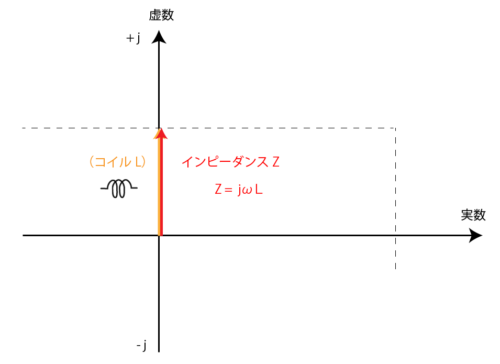
コイルは jωL の部分ですが、角周波数の ω が ω =2πf となるため、周波数に比例してインピーダンスが高くなります。ちなみに直流の場合 f = 0 となるので、コイルのインピーダンスは 0 、つまり短絡・ショートとなります。
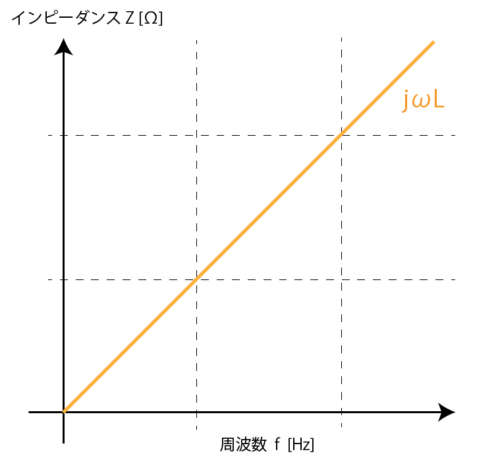
インピーダンス特性は右肩上がりのグラフとなります。
コンデンサ
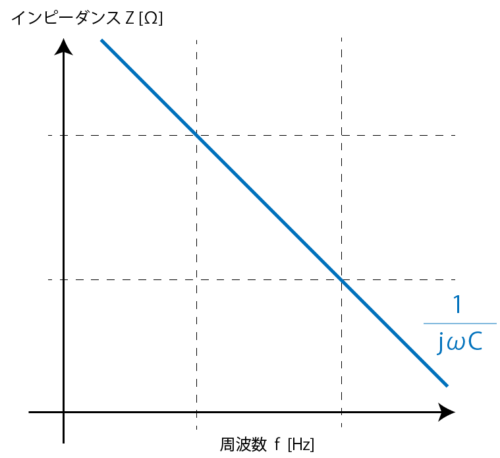
コンデンサは 1/jωC の部分で、周波数に比例してインピーダンスが低くなります。コンデンサは直流の場合、インピーダンスが ∞、つまり開放・オープンとなります。
抵抗、コイル、コンデンサのそれぞれのインピーダンス特性は、電気・電子回路の特性を理解する上で非常に重要となります。
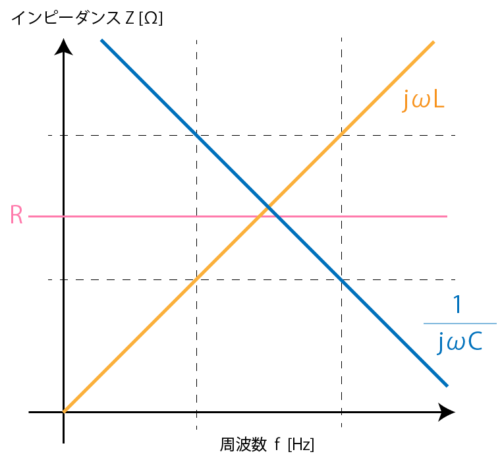
式をもとに理解するのが難しいという方も、インピーダンス特性のグラフの特徴だけは必ず覚えておくことをおすすめします。

おわりに
今回は電気回路の基本となる「インピーダンスの基礎」と「抵抗」「コイル」「コンデンサ」のインピーダンス特性について解説しました。
- インピーダンスは交流の電流の流れにくさを表す
- 抵抗のインピーダンスは一定
- コイルのインピーダンスは周波数に比例
- コンデンサのインピーダンスは周波数に反比例
いずれも電気回路においては非常に重要な内容なので、インピーダンス特性のグラフの特徴とともに理解しておく必要があります。
今回は以上です。
最後までお読みいただき、ありがとうございました。