伝送線路の反射の実態

この記事では、伝送線路の反射をインピーダンスマッチングの話を交えて解説します。
動画はこちら↓
伝送線路の反射とは
高周波、あるいは高速のデジタル信号においては、伝送線路の長さに対して信号の波長が短いため、信号を波として捉える必要があります。
このような回路を、分布定数回路と呼びます。
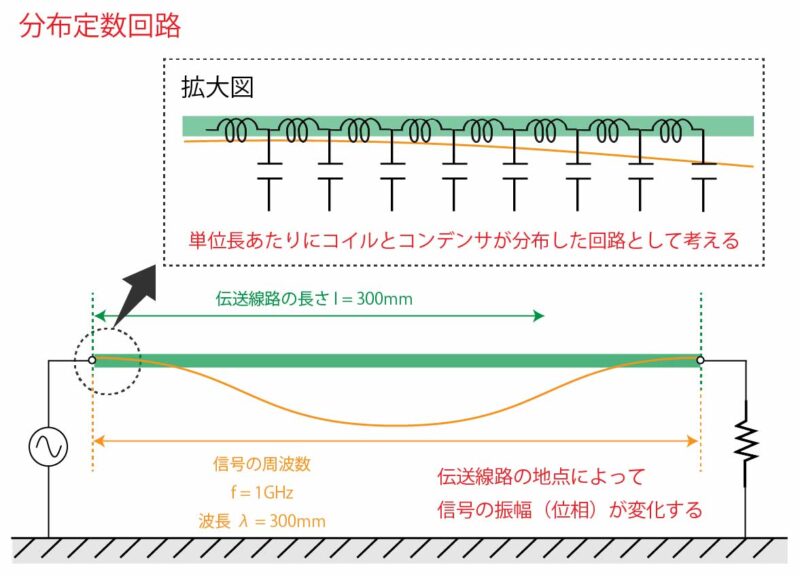
ここでは QucsStudioを使って、伝送線路の反射の影響を確認してみます。
反射の検証モデル
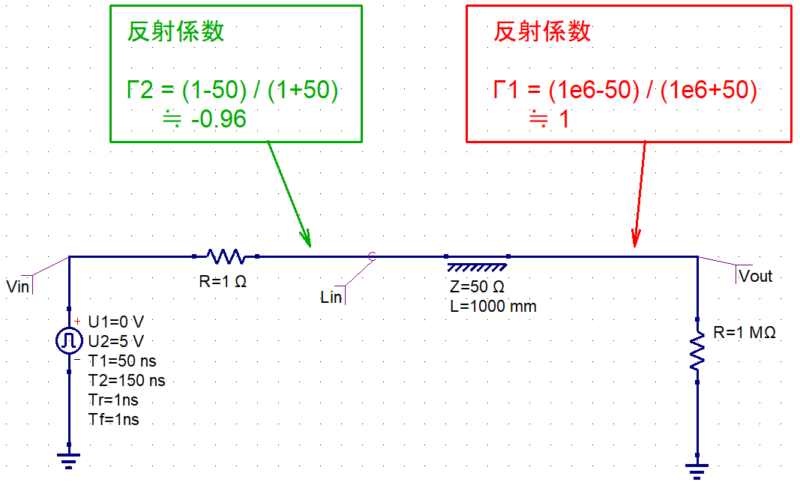
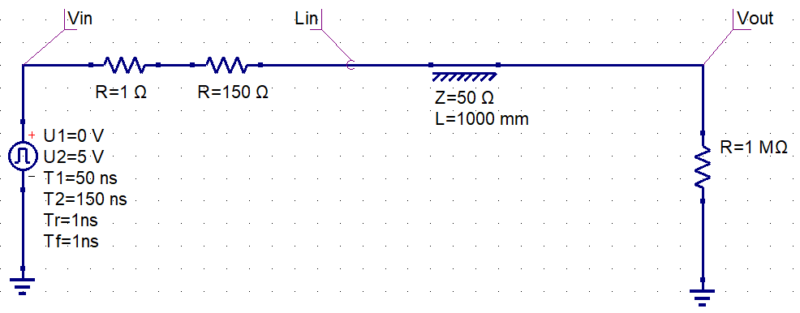
特性インピーダンスと長さを規定した伝送線路「Transmission Line」に、信号源、出力抵抗、負荷抵抗を接続します。
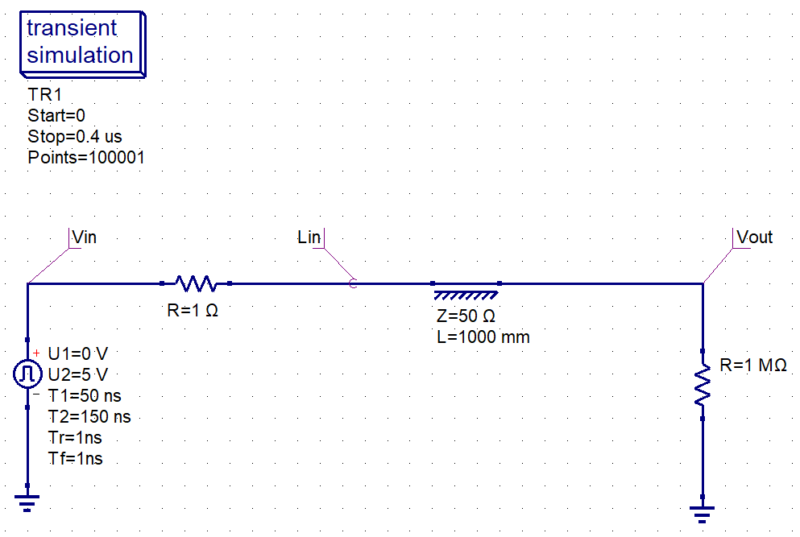
信号源は立上り・立下り時間が 1ns、パルス幅が 100nsと設定し、そこに 1Ωの出力抵抗と特性インピーダンスが 50Ωの 1mの伝送線路、そして デジタルICの入力ピンに相当する
1MΩの抵抗を直列に接続しています。
この回路で負荷電圧 Voutは、伝送線路と負荷のインピーダンスが整合していないために反射が発生し、電圧波形が一定周期で振動します。
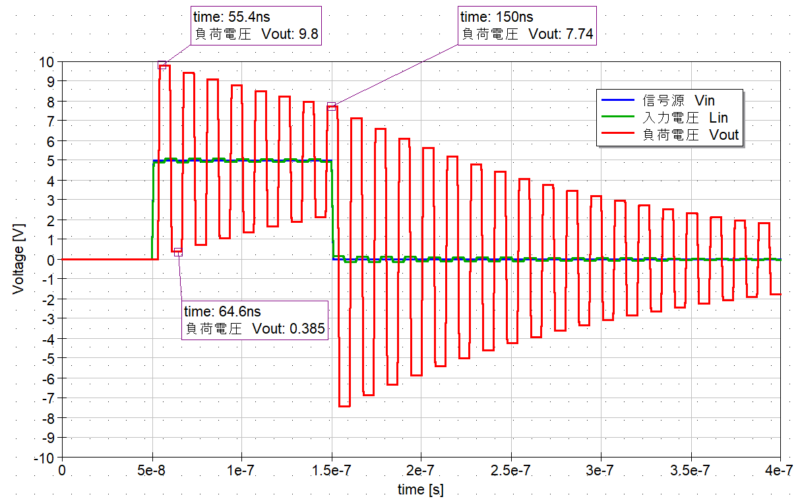
このように伝送線路の特性インピーダンスに対して、出力インピーダンスや負荷インピーダンスが整合していない場合には、それぞれの不整合点で信号が反射して信号波形が暴れてしまうような現象が発生します。
集中定数回路での振る舞い
ちなみに、集中定数回路で表せるような低速信号の場合、同じ回路でも反射の影響は見えなくなります。

つまり集中定数回路においては、インピーダンスマッチングを気にする必要はないということです。

反射係数の計算
ここでは、反射係数をもとして反射の影響度を計算してみます。
反射係数というのは、インピーダンスの不整合によって発生する反射の程度を表すための係数で、伝送線路の特性インピーダンス Z0 と負荷のインピーダンス ZL の和分の差として求めることができます。
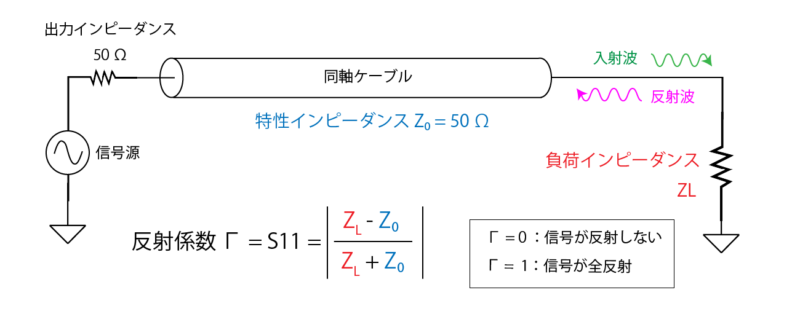
先ほどの回路で考えると、特性インピーダンスが 50Ωの伝送線路に対して 1MΩの負荷が接続されていたので、反射係数 Γ≒1(全反射)となります。

ここで発生する反射波は、入力電圧 5Vがそのまま反射する、つまり 5Vが足し合わされるように作用するため、負荷の電圧は入力電圧に対して 2倍の 10Vになります。
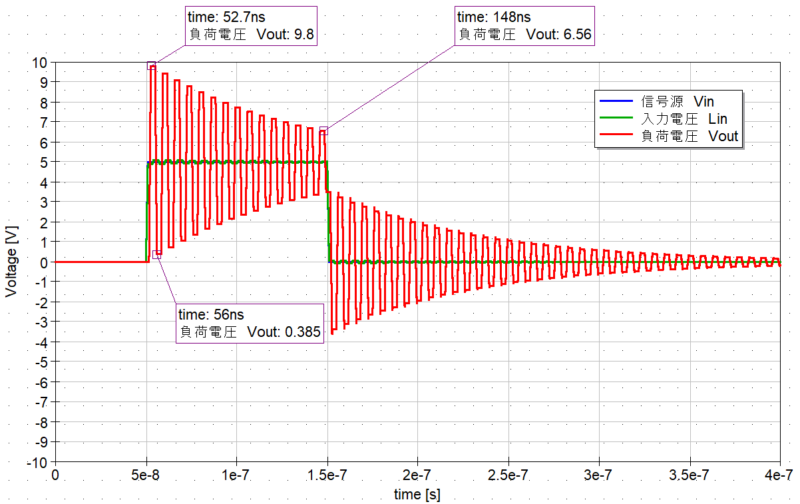
波形を見てみると、反射係数の計算で求めた通り入力電圧 4.9Vに対して約2倍の 9.8Vまで上昇しています。

この伝送線路の反射は、負荷だけでなく出力側でも発生します。
具体的には、 50Ωの伝送線路と1Ωの出力抵抗の間で信号が反射し、ここでの反射係数は Γ≒-0.96 となります。
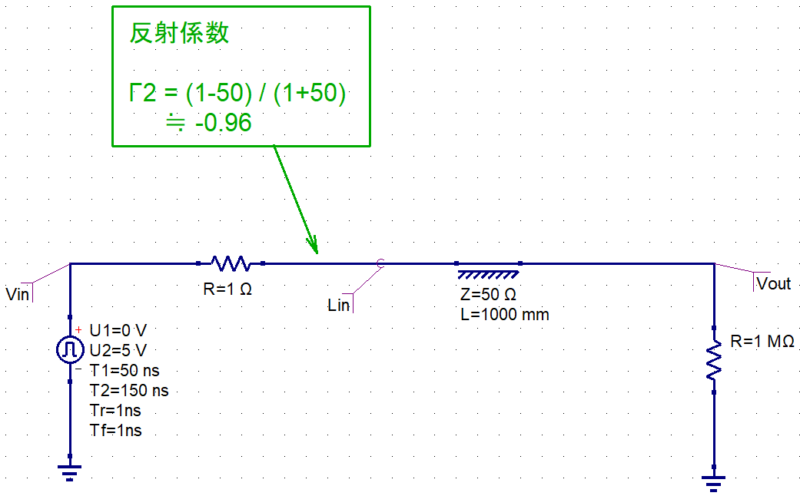
そのため、4.9Vの反射波に対して -4.7Vの再反射波が発生し、さらに再反射波が入力電圧と足し合わされることによって、負荷電圧は約 0.3Vになります。
このように伝送線路を挟んで、繰り返し反射が発生することを多重反射と呼びます。
この多重反射が発生すると、それぞれの反射係数によって電圧が徐々に低下していくものの、信号品質という観点では多重反射を発生させないことが重要になります。
ちなみに、多重反射による電圧変動は一定期間ごとに発生していますが、これは伝送線路の信号の伝搬速度、つまり伝送線路の長さによって変わります。
例えば長さを1mの半分の 50cmとすると、この間隔が半分になります。

反射の抑制方法
一般的な反射の抑制方法として、よく知られているのがインピーダンスマッチングです。
インピーダンスマッチングには、コイルとコンデンサを使って特定の周波数でのみインピーダンスを整合させる方法もありますが、ここではダンピング抵抗によるインピーダンスマッチングについて解説します。
反射抑制の原理
伝送線路の反射は、特性インピーダンスZ0と負荷インピーダンスZLが一致している場合に最小 Γ=0 になります。
つまり、特性インピーダンスと負荷インピーダンスを一致させるように回路を調整すれば良いということです。
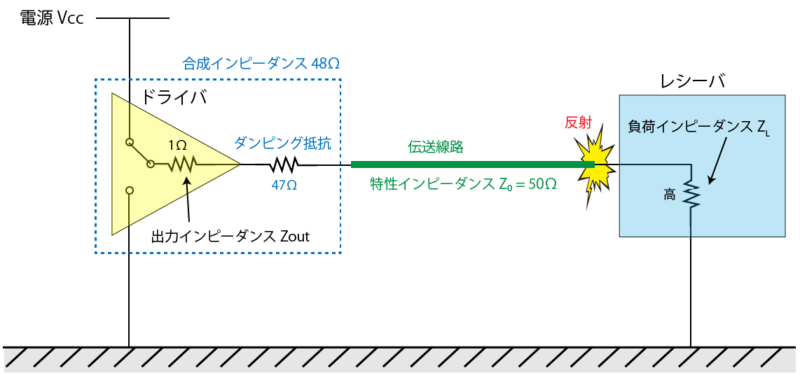
出力側で回路を調整する場合、ドライバの出力抵抗に対して直列に抵抗を接続して、この合成抵抗が伝送線路の特性インピーダンスと一致するようにします。
具体的には、47Ωの抵抗を直列に接続した場合は合成抵抗が 48Ωとなり、このときの反射係数は Γ=-0.02となります。
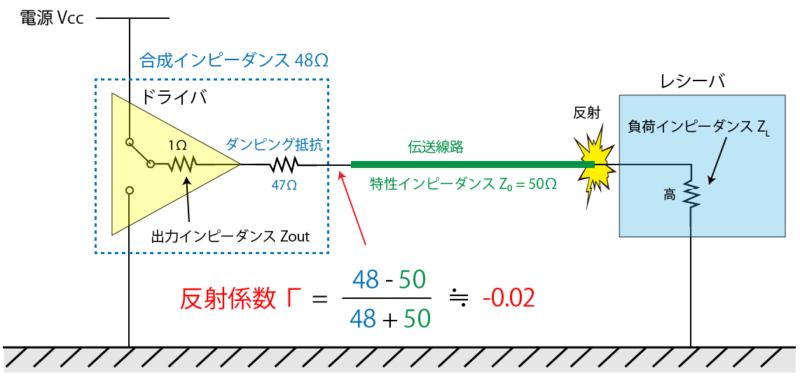
つまり、信号がほとんど反射しないということです。
そのため、この回路に信号を入力しても多重反射によるリンギングは発生せず、きれいなパルス波として信号が伝送されます。
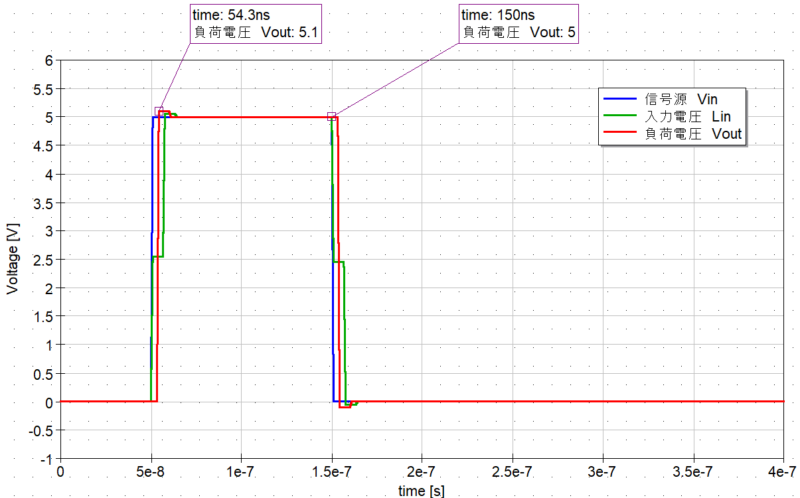
これがダンピング抵抗によるインピーダンスマッチングの効果です。

ダンピング抵抗の原理
ダンピング抵抗の効果を確認するために、伝送線路の長さを 3mに変更してみます。
すると、レシーバ側で全反射して2倍の電圧になっていることは同じですが、入力電圧がもとの約半分の 2.5Vになっていることがわかります。
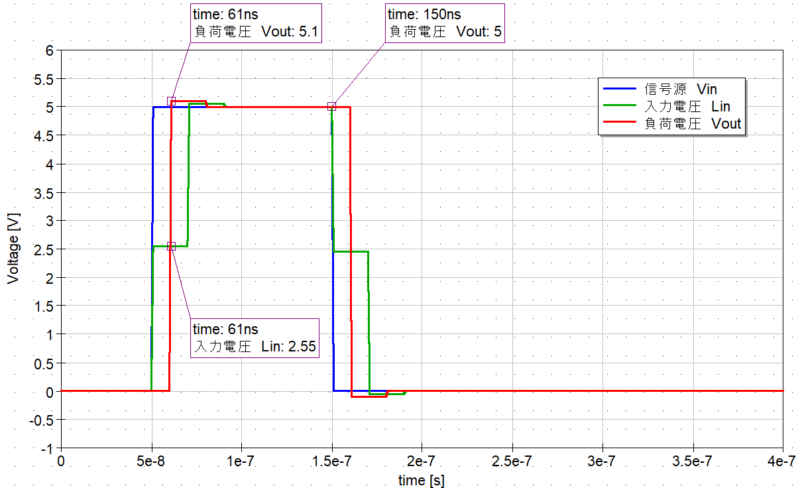
これは、ドライバ側の合成抵抗と伝送線路の特性インピーダンスによって入力電圧 5Vが分圧されているためです。
この回路の場合は、48Ω:50Ωで分圧されることによって、負荷への入力電圧が 2.5Vまで低下しています。
そして、この2.5Vの入力電圧が負荷とのインピーダンスの不整合によって全反射し、2倍の 5Vの電圧として観測されます。
さらに負荷で発生した反射波は、伝送線路を介して反対側の出力側へと伝搬していきますが、出力側ではインピーダンス整合しているために反射波はほとんど発生せず、負荷に掛かる電圧は 5Vのまま安定します。
つまり、信号に不要なリンギングが生じないということです。
ダンピング抵抗の作用
ダンピング抵抗の原理で分圧が出てきましたが、これはダンピング抵抗の効果としてよく言われる、波形をなまらせる効果にもつながっています。
例えば、ダンピング抵抗の抵抗値を 150Ωとすると、再びインピーダンスの不整合が発生することで多重反射する波形となります。
このときの波形は、ダンピング抵抗と特性インピーダンスの分圧によって入力電圧が 1.24Vまで低下しますが、多重反射することによって徐々に電圧が上昇していき、最終的には信号源と同じ 5Vに収束していきます。

この現象を言い換えると、多重反射を利用して信号の立上りを鈍らせていると言うことができます。
これがダンピング抵抗が、波形を鈍らせる働きを持つと言われる所以です。
ちなみ、実際の回路においては負荷が寄生容量を持つため、信号波形が緩やかに上昇するような鈍った波形となります。

おわりに
今回は伝送線路の反射をテーマに、反射の原理とダンピング抵抗を使ったインピーダンスマッチングの効果を解説しました。
高周波回路の反射は、目に見えないために中々理解しづらいところもありますが、回路シミュレータを使うことで視覚的に反射の影響を学ぶことができます。
今回の解説した回路は、どれも非常に簡単に作れるものばかりなので、興味のある方はぜひ自分自身でも検証してみてください。
インピーダンスマッチングについては別の記事でも解説しているので、そちらも参考にしてみてください。


今回は以上です。
最後まで読んでいただき、ありがとうございました。